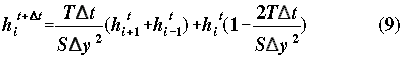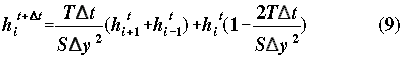The
EXPLICIT SOLUTION was given as equation 9 on the finite difference main
page:
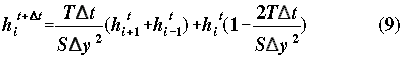
to ensure stability:

so use 0.07 days and note that you can solve for head at any node by:

for the first time step:

- volume of flow into the left boundary for time
step is:
- VOLleft
= Q dt = Ti dx DT
- VOL = 0.06 ft2/d (h1-h2)/y
dx DT
- = 0.06 ft2/d * (8.2-8.2)ft/3ft * 1 ft * 0.07d = 0 ft3
- volume of flow out of the right boundary is:
- VOLright
= Q DT = Ti dx DT
- VOL = 0.06 ft2/d (h4-h5)/dy
1 ft 0.07d
- = 0.06 ft2/d (6.06-3.6)ft/3ft 1 ft 0.07d = 3.4x10-3 ft3
- the change in storage all occurred in cell 4:
- Change in
S4 = (h40-h40.07)*S*dx*dy
- =
(8.2ft - 6.06ft)*0.001*(3ft2) = 6.4x10-3 ft3
- Mass Balance
- Mass Balance = (Inflow - Outflow) / ((Inflow+Outflow) / 2)
- water coming out of storage is seen as an
inflow
- (6.4x10-3 ft3
- 3.4x10-3 ft3) / 4.93-3 ft3
= 0.61
- does
not look good!
using the heads from time = 0.07 to solve
for
heads at time = 0.14:
- h1 through h5 are: 8.2
8.2 8.2 6.06 3.6

- VOLleft
= 0
- VOLright =3.2x10-3 ft3
- Change in Storage (cells 3 and 4) =3.4x10-3 ft3
- Mass Balance = 0.06
-
- the mass balance is looking better
using the heads from time = 0.14 to solve
for
heads at time = 0.21:

and so on ...
Notice that given the character of the explicit equations the pressure
front can
only move one cell at a time, consequently large time steps lead to
fairly large
inaccuracies in the solution
You may wish to explore the following exercise related to the material
you just
studied now, in which case follow the steps below. Otherwise continue
the discussion
for this unit by going "BACK" and exploring the implicit option, then
take up
the exercises later when you reach the exercise section on the main
page for this
unit.
For the same parameters you were using above:
1. Calculate h4 @ 0.07 day increments to 0.7 days using the
explicit
approach
2. Repeat #1 @ 0.14 day increments to 0.7 days using the explicit
approach
3. Graph your results as head vs time
4. Explain what you see