K = 1 ft/day L = 100 ft h1 = 103 ft h2 = 93 ft
UNCONFINED:
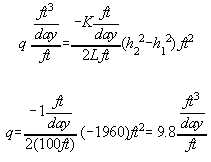
Q = 9.8 ft2/day
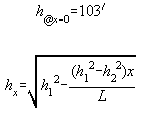
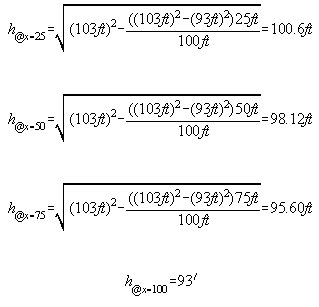
h @ x=0' x=25' x=50' x=75' x=100'
103' 100.6' 98.1' 95.6' 93'
CONFINED FLOW EQUATIONS:
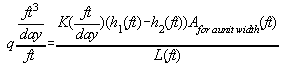
assume average thickness equal to the average h (103+93)/2 to be consistent with the Dupuit conditions
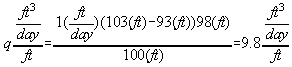
Q = 9.8 ft2/day
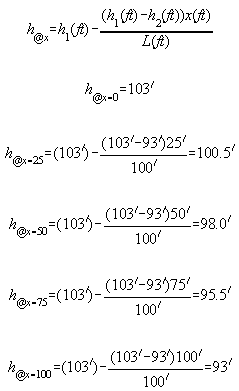
h @ x=0' x=25' x=50' x=75' x=100'
103' 100.5' 98.0' 95.5' 93'
COMPARE UNCONFINED & CONFINED RESULTS: q is the same
h@x=0 and h@x=100 are the same
h@x=25 unconfined = 100.6' confined = 100.5'
h@x=50 unconfined = 98.1' confined = 98.0'
h@x=75 unconfined = 95.6 confined = 95.5'
UNCONFINED IS ALWAYS HIGHER THAN CONFINED - DOES THIS MAKE SENSE? YES, DUE TO PARABOLIC FORM OF WATER TABLE SURFACE. If this isn't clear, sketch the system with the fixed heads on both sides and draw a straight line between them. Now try to draw another line with the end points at the same place but connect them with a line that is always increasing in slope from left to right (to allow the same q through a smaller flow area) or, think of it as an everywhere concave downward line. You will see that the position of this latter line will be above the first line everywhere, except at the end points where they are equal.
How will the results change (and compare) if the system is as follows?
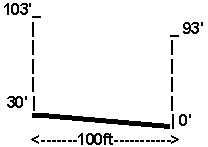
For the UNCONFINED calculation, one either needs to express the heads using the aquifer bottom as the datum in which case the gradient will be in error, or the previous heads are used, in which case the flow thickness is in error. We will use the same heads as previously used which will result in a saturated thickness error, but the results remain the same as calculated using the Dupuit equations above
Q = 9.8 ft2/day
h @ x=0' x=25' x=50' x=75' x=100'
103' 100.6' 98.1' 95.6' 93'
For the CONFINED system use the average thickness to determine the flow area (to stay similar to previous assumptions, take the 98' thickness that was used previously, subtract the 30' from the left side, average 68' & 98' feet to get 83'):
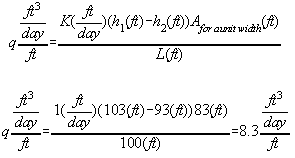
Q = 8.3 ft2/day
This change in flow thickness does not affect the head calculation under confined conditions, so the heads remain:
h @ x=0' x=25' x=50' x=75' x=100'
103' 100.5' 98.0' 95.5' 93'
COMPARE UNCONFINED & CONFINED RESULTS for the SLOPING AQUIFER:
head results do not change from previous analysis
q differs by 15%
the slope of the aquifer causes the Q to be in error
If we use the same flow thickness, we will get the same answer. The flow thickness is determined automatically when using the Dupuit equations because h reflects the physical dimensions of the flow field. For the confined situation, h only reflects the gradient. Be cautious when using the Dupuit equations, to be sure that the datum used to measure head reflects the base of the aquifer and that the base of the aquifer is approximately horizontal.
... later you could check your comparison by using a numerical model to make these same calculations