
What concentration would we expect to see if a water sample a piezometer 16 inches to the right of the reservoir after 2 1/2 minutes?
For your convenience, I include the appropriate expression here:
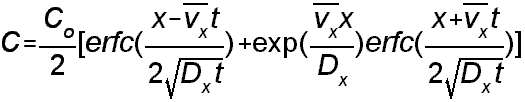
where:
Co = source concentration [M/L3]
C = concentration [M/L3]
x = distance from the source in the direction of flow
t = time since continuous concentration release began [ T ]
Dx = dispersion coefficient in the x direction [L2/T ]
erfc = the complimentary error function ERFC
Calculate your answer, being extremely careful with respect to using consistent units and noticing how the answer is expressed (e.g. as Concentration or relative Concentration, then check yourself by deciding whether the answer is reasonable, and visiting the key. If you want to know if your answer is correct before viewing the key, click answer for the value.