For your convenience, I include the appropriate expression here:
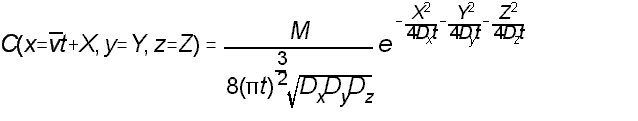
where:
C = concentration [M/L3]
x, y, z = are orthogonal distances from the initial position of the mass
X, Y, Z = are orthogonal distances from the center of mass
t = time since mass was released [ T ]
M = mass introduced at time 0 at x=y=z=0
Dx, Dy, Dz = dispersion coefficients in the x, y, & z directions [L2/T ]
- Note: dispersivity varies with scale of plume migration, as well as, direction and each dispersivity is multiplied by the velocity in the x direction
Calculate your answer, being extremely careful with respect to using consistent units, then check yourself by deciding whether the answer is reasonable, and visiting the key. If you want to know if your answer is correct before viewing the key, click answer for the value.
