BOUNDARY CONDITIONS

MT3D includes:

specified concentration which may vary with time (Dirichlet Condition)

This is an infinite source or sink of mass. The rate of dispersive mass flux is controlled by the difference in concentration that is fixed and the concentration calculated in the adjacent node. The advective flux of mass across the boundary will be the product of the volumetric flux of water and the specified concentration.

fixed concentration gradient (fixed mass flux) across a boundary (Neumann Condition)

This defines the total flux of mass (both advective and dispersive). A no-flow boundary representing impermeable material is also a ZERO mass flux boundary because there is no advection or diffucion into the material. .

concentration dependent flux, or "combined" boundary (Cauchy Condition)

In this case both the concentration and the gradient are fixed, so that both the dispersive flux and the advective flux are individually defined. For impermeable boundaries, both the concentration and the gradient are zero. On inflow and outflow boundaries it is often assumed that advection dominates and can be simplified to a Neumann boundary.

EXAMPLE:

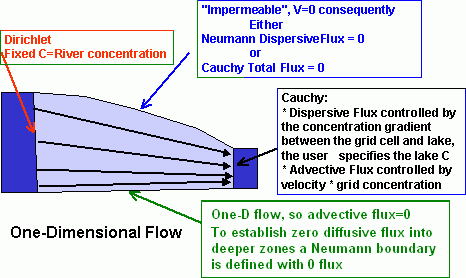
A common problem with transport boundary conditions is as follows:

A modeler wants to represent the growth of a plume in a pristine aquifer from a source with a constant concentration of 1000ppm.

It is common for the modeler to set initial conditions to zero concentration everywhere and define a Dirichlet boundary with a fixed concentration of 1000 at the node where the source is located

This generally leads to "crazy" answers ranging from the model crashing to contaminant occupying the entire grid on the first time step, to instability in the solution.

It is better to use a boundary that more accurately reflects the true sequence of events in the field.

There wasn't suddenly a concentration of 1000 filling the subsurface in a volume equal to the entire volume of the grid cell with abrupt drops to zero yielding an infinite concentration gradient

An alternative approach is to represent the infiltration that carries the contaminants into the subsurface and specify a concentration for that water.

In this case the concentration slowly increases in the source cell and begins to migrate outward.