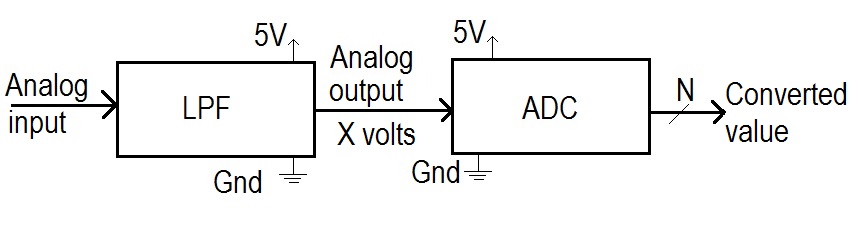
- Aliasing:
You're sampling an analog signal at 20kHz. List all the frequencies in the first four harmonics that will look like 2kHz signals.
1st harmonic: 2kHz 20kHz-2kHz = 18kHz
2st harmonic: 20kHz+2kHz=22kHz 40kHz-2kHz = 38kHz
3st harmonic: 40kHz+2kHz=42kHz 60kHz-2kHz = 58kHz
4st harmonic: 60kHz+2kHz=62kHz 80kHz-2kHz = 78kHz
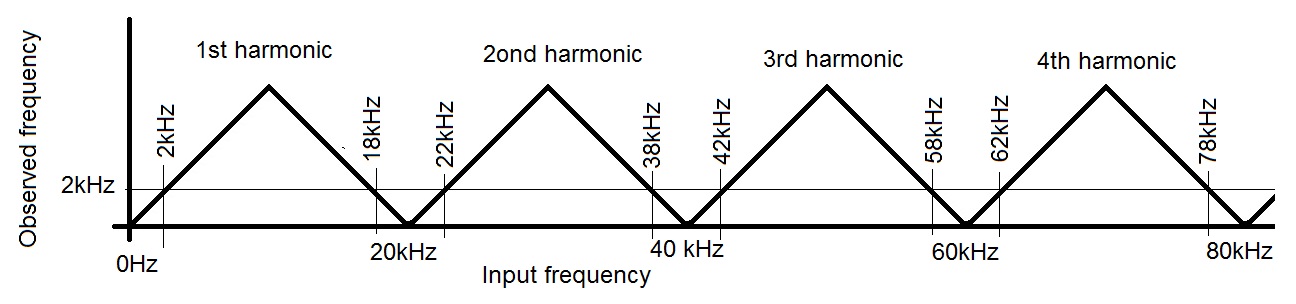
- Decades:
A first-order LPF has a cutoff frequency of 2kHz. Describe
the attenuation of an 80kHz input signal in decibels and as
a ratio of output voltage to input voltage.
Since a decade is a multiplicative factor of 10, we need to find how may powers of 10 you have to multiply 2 to get 80. In order words:
2*10x = 80, solving for X yields
x = log10(80/2) = 1.6
So we know that a 80kHz waveform is 1.6 decades above a 2kHz waveform. Since the LPF attenuates -20dB/decade, the 80kHz waveform will be attenuated:
1.6*-20 = -32dB
Decibels can be converted to the ratio of output/input using its definition.
-32dB = 20dB log_10(Vout/Vin)
Vout/Vin = 0.025 = 1/40
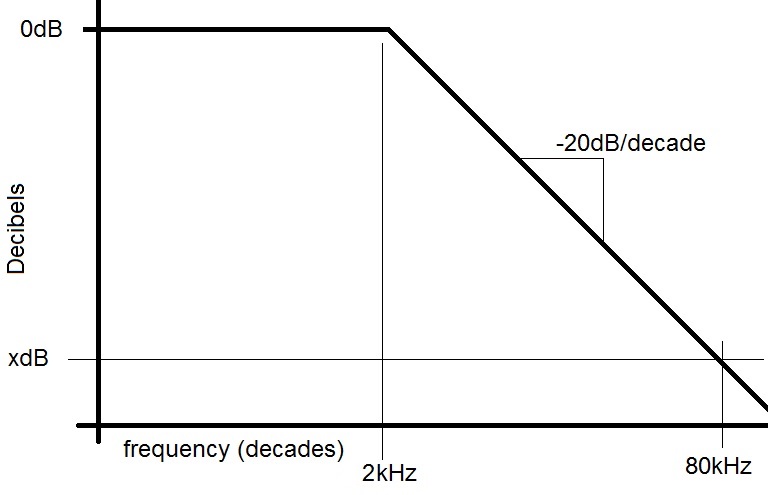
- ADC convert:
You're working with a N-bit ADC and would like to attenuate a full scale
input to a voltage that has a converted value below 1/2 LSB. How many dB
will be required to achieve this?
The hardware diagram below explains visually what this problem is asking. The LPF needs to reduce a full scale (5 V) input to a voltage X that has a converted value of 0.5 bits. We have already looked at this concept when we covered quantization error.
5 V X v 5 V
--- = --- X V = ----
2N 0.5 2N+1
This is the input voltage to the ADC which generates 0.5 bit output. But it is also the output of the LPF when a full scale input (5 V) is applied. So the LPF needs to attenuate a 5V input into X V. Let's see how many decibels that works out to.
(5 V / 2N+1)
20 log10 ----------- = 20 log10(2-(N+1))
5 V