The IMPLICIT SOLUTION was given as equation 11 on the finite difference main page



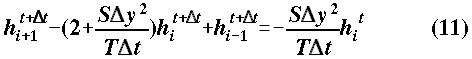
using the same time step as we used for the explicit approach, 0.07 days and noting that we now have 3 unknowns in each equation so we cannot solve for head at each node separately as we did with the explicit solution, rather we have to solve all 3 equations simultaneously. Noting the values of the constants:

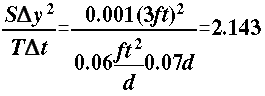  and  

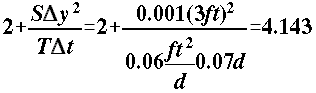
for the first time step write the finite difference equations for each of the unknown heads at cells 2, 3, and 4:



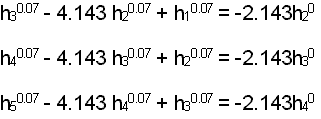
rearranging so that the same nodes fall in columns and substituting 8.2 for cell 1 and 3.6 for cell 5:



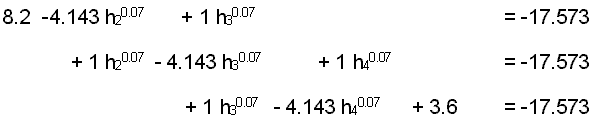
subtracting 8.2 from both sides of the first equation, subtracting 3.6 from both sides of the third equation, and expressing the equations in matrix notation:



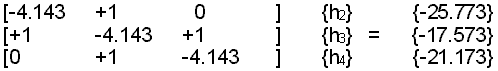
recall:





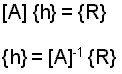
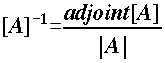
the adjoint [A] = transpose of the cofactor of [A]

each element of the cofactor matrix is the determinant of remaining values after that row and column are crossed out with a sign change if the sum of the subscripts is odd



thus the cofactor of A is:



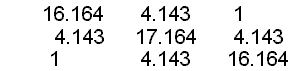
transposing involves interchanging rows and columns, but there is no change when you do this to a symmetric matrix

determinant of [A] = |A| = is sum the products of the right diagonals (-71.112, 0, 0) minus the products of the left diagonals (0, -4.113, -4.113)



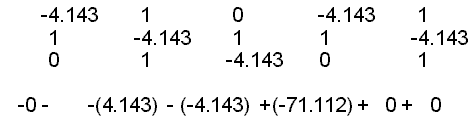
or:

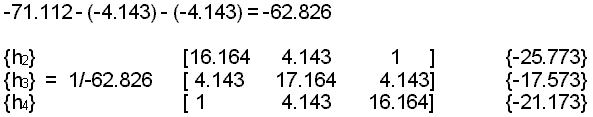         note this is: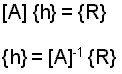


carrying out the arithmetic:



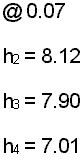
as outlined in the explicit solution:

Q_left = 1.12x10^-4 ft³

Q_right =4.7774x10^-3 ft³

Flow in from storage (cells 2, 3, and 4) =4.71x10^-3 ft³

Mass Balance = 0.01

the mass balance is looking much better for a first step of the same length using the implicit rather than explicit approach

and so on ...

You may wish to explore the following exercise related to the material you just studied now, in which case follow the steps below. Otherwise continue the discussion for this unit by going "BACK" twice and exploring alternative formulations, then take up the exercises later when you reach the exercise section on the main page for this unit.

For the same parameters you were using above:

1. Calculate h₄ @ 0.07 day increments to 0.7 days using the implicit approach

2. Repeat #1 @ 0.14 day increments to 0.7 days using the implicit approach

3. Compare the mass balance at each step for the 0.07 and the 0.14 day time steps.

4. Graph your results as head Vs time

5. Compare your result to those from the explicit method