UNIT
13 -- INTRODUCTION TO CONTAMINANT TRANSPORT MODELING:
As in previous units, I assume that your
are familiar with the fundamentals of contaminant transport from previous
ground-water courses, and that now, the issue is how to represent the process
numerically. However, if you would like a brief review of subsurface contaminant
transport and simple analytical solutions, then revisit
Unit 5.
Unlike the ground-water flow equations, one term
of the advection-dispersion equation includes a first partial derivative while
the other includes a second partial derivative.
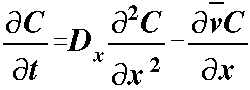
Mathematicians refer to the character of the dispersion
term as parabolic, while the advection term is hyperbolic. This leads to difficulty
in obtaining a numerical solution
The OBJECTIVE of UNIT 13 is for you to:
* BECOME FAMILIAR with ALTERNATIVE METHODS for SOLVING the ADVECTION-DISPERSION EQUATION
* BECOME AWARE of the SPECIFIC ITEMS that must be CONSIDERED for TRANSPORT MODELING
DISCUSSION
The hyperbolic form of the partial differential equation describing the advection-dispersion process known as the ADE (Advection Dispersion Equation) makes it difficult to accurately simulate the advection-dispersion process.NUMERICAL METHODS FOR CONTAMINANT TRANSPORT
EXERCISES
If
you chose to purchase Applied Contaminant Transport Modeling,
If you chose to purchase Applied Ground-water Modeling,
If you chose to purchase Introduction to Ground-water Modeling,
Read about methods for solving the ADE in the MT3D
manual which can be down loaded from http://hydro.geo.ua.edu/
under MT3D Resources. COMMUNICATION Please
bring up any questions you may have about regarding contaminant transport
modeling. epoeter@mines.edu
ON TO LESSON 14
BACK TO LESSON LIST
BACK TO MAIN PAGE