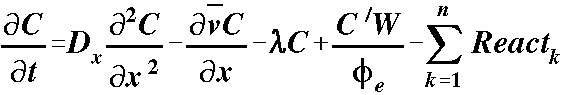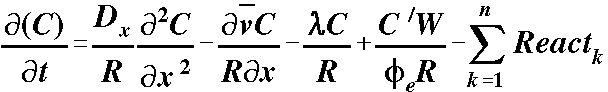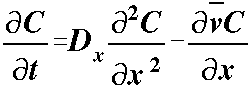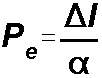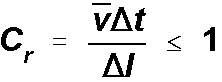The full ADE (advection-dispersion equation) in one-dimension,
including source/sink terms and simple reactions can be written as:
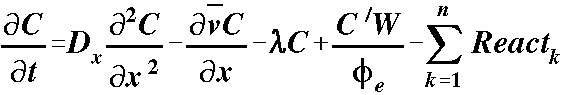
dispersion advection
decay src/sink reactions
- If
retardation is considered we have:
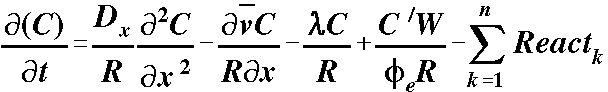
Unlike the ground-water flow equations, one term of the advection-dispersion
equation includes a first partial derivative while the other includes a second
partial derivative.
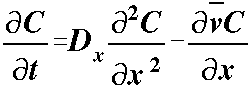
The dispersion term is parabolic, while the advection
term is hyperbolic. This leads to difficulty in obtaining a numerical solution
ISSUES TO CONSIDER WHEN SOLVING THE ADE
INCLUDE Framework, Grid Design, and Solution Scheme:
FRAMEWORKS for solving
the ADE (advection-dispersion equation)
Approaches
to solving the ADE can be divided into Eulerian, Lagrangian, and Mixed Eulerian-Lagrangian
methods. They each have advantages and disadvantages.
Global guidance for DESIGNING
GRID and TIME STEPS sizes:
When
Advection dominates dispersion, designing a model with a small (<2
but sometimes as high as 10 will yield acceptable results)
Peclet Number will decrease oscillations, improve accuracy & decrease numerical
dispersion.
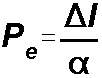
When Advection dominates dispersion, designing a model with a small
(<1) Courant Number, which reflects the portion of
a cell that a solute will traverse by advection in one time step, will decrease
oscillations, improve accuracy & decrease numerical dispersion.
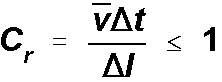
-
In some
codes Upwind Weighting is available to decrease
overshoot/undershoot and in some formulations the numerical dispersion,
this is accomplished through use of non-symmetric weighting functions on
the concentration at each node
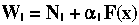
-
The modeler selects the degree of upwinding where
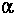 ranges from 0 to 1
ranges from 0 to 1
SOLUTION SCHEME
Solution methods commonly
employed for solving the ADE
(advection-dispersion equation) include Finite Difference,
Finite Elements, Random Walk, and Method of Characteristics.
Each has advantages and disadvantages.