The flow equation is solved first by some means and the interfacial velocities are provided to the transport model. For transient flow problems this is coupled by solving a time step for the flow solution and then solving the transport equation for that time period. The nature of the transport solution often requires that a number of smaller time steps are undertaken for the transport simulation within a constant flow system that prevails for that time step.
Finite Difference
- The same fundamental finite
difference concepts apply to transport simulation as were discussed in unit
6. The specifics of the formulation will not be addressed
here. An excellent discussion is given by Zheng and Bennett in Chapter 6.
Further discussion of the Finite Difference Method for contaminant transport
simulation can be reviewed in the MT3D manual by Zheng and Wang. Finitie difference
schemes for transport suffer from humerical dispersion and oscillation, but
conserve mass.
Recently, solution techniques collectively referred to as total-variation-diminishing methods (TVD) have provided a higher-order Finite Difference method that are robust, minimizing numerical dispersion and, when implemented with procedures called flux-limiters, they eliminate spurious oscillations while preserving sharp concentration fronts. TVD refers to the property where the sum of concentration differences between adjacent nodes diminishes over successive transport steps. When compared with commonly utilized Lagrangian and mixed Eulerian-Lagrangian methods (e.g. Method of Characteristics), TVD schemes are not as effective in eliminating numerical dispersion while preserving sharp concentration fronts and concentration peaks, but their ability to conserve mass and their smaller memory requirements make them an excellent choice for simulating subsurface contaminant transport.
- Finite Element modeling is very similar to finite difference modeling and is rather invisible to the modeler with the exception of the character of the input data. Finite elements use a smooth function to describe variation between location whereas the finite difference method uses a step function. Spatial formulation is more flexible in finite element models and, as such, problems can be solved with far fewer nodes than a finite difference formulation, but generally the increased computational requirement lead to similar computing time requirements for the two formulations. The specifics of the finite element formulation will not be addressed here. Again, an excellent discussion is given by Zheng and Bennett in Chapter 6.
- The random walk method is Lagrangian
method that is free of numerical dispersion and provides
perfect mass balanced results. It is simple and efficient. The major drawbacks
are the discrete nature of the solution which requires a bit of thoughtfulness
to properly interpret and potential problems of needing small time steps in
highly heterogeneous media.
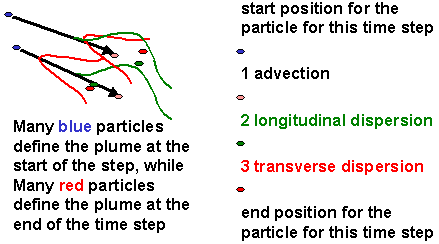
Given the velocities at every cell interface from a flow solution- A large number of particles are simulated to represent contaminants
- Each particle represents a given mass
- Concentration is calculated as:
- (#particles) * (particle mass) / (volume of zone)
- For every time step:
- each particle is advected to a new
location using velocities interpolated for the flow simulation
- then each particle is randomly repositioned using a normal distribution and the dispersion coefficients of the aquifer
- If the time step is too large and the flow field is variable, the path will be in error
It can take a very large number of particles to capture the important features of a system in a complex system, which may require large amounts of computer memory, storage, and time. - then each particle is randomly repositioned using a normal distribution and the dispersion coefficients of the aquifer
Please explore this sample Random Walk Simulation.
For more detail on the random walk approach, see Zheng and Bennett, Chapter 6. - A large number of particles are simulated to represent contaminants
- The Method of Characteristics is a mixed
Eulerian-Lagrangian method that substantially reduces
numerical dispersion , but can suffer from substantial mass balance problems.
Given the velocities at every cell interface from a flow solution- Packets that represent concentration
rather than mass (mass is represented by particles in random walk) are tracked
- In a global sense, for every time step:
- Packets are advected
- In a global sense, for every time step:
- Cell concentrations are determined from the concentration of packets in each cell
- Finite difference is used to calculate dispersion and the concentrations are adjusted
- Packets that represent concentration
rather than mass (mass is represented by particles in random walk) are tracked