The Method of Characteristics is a mixed Eulerian-Lagrangian method that substantially reduces numerical dispersion, but can suffer from substantial mass balance problems.
The Eulerian expression of the solute transport equation (ADE advection-dispersion equation) in one-dimension, including source/sink terms and simple reactions is as we have been viewing it with respect to concentration changes with time at a fixed point in space:
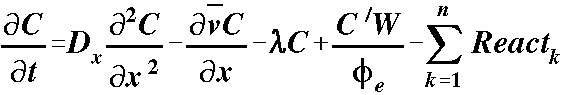
dispersion advection decay src/sink reactions
- By the chain rule
(the derivative of a product is equal to the first term times the derivative
of the second term plus the second term times the derivative of the first
term), we can express the advective
term of the ADE as:
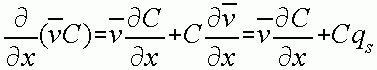
The q is the source sink term in a steady situation, or in a transient situation the source/sink plus the water in from or out to storage. In an alternative Eulerian form we consider the "rest" of the expression plus the advective portion:
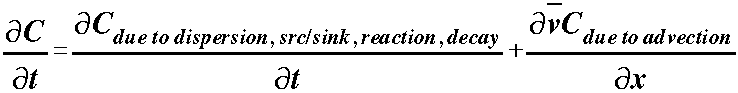
The "rest" of the expression is independent of the advection, thus is readily solved by finite differences:
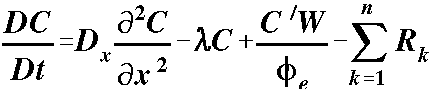
For the advective portion of the calculation, we work in a coordinate system that is relative to the packets rather than the grid, as if we were "riding" on a packet. This represents the rate of change of C along a pathline followed by a particle (a characteristic curve of the velocity field), so the discrete change in concentration as a function of time is the difference between the concentration at the next time step and the concentration due only to the advection:
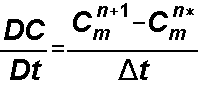
where:
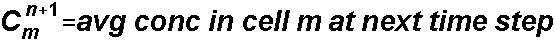
(this is what we are striving to solve for)
and
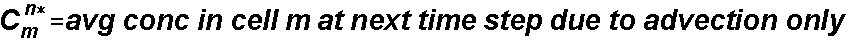
rearranging we can write the change in concentration due to everything but advection as:
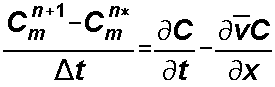
diff in future C less = total change - change due to
that due to advection concentration advection
rearranging to put the item we are solving for on the left:
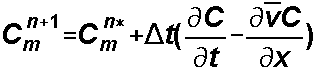
so:

while:
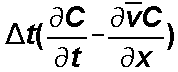
accounts for dispersion, source/sinks, and reaction and is solved by finite differences on a fixed grid - the Eulerian approach
As written above, the final concentration for the cell at the end of the time step includes the contribution from both the Eulerian and Lagrangian steps
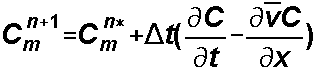
new C = Lagrangian + Eulerian
- 1. packets are distributed over the
flow domain, each has a concentration and x,y location
- 2. packets are tracked forward using velocities based on head differences and K's and a small time step
- 3. an "intermediate" concentration in each cell is calculated as the average of concentration of the packets in the cell (introduces some numerical dispersion)
- 4. a weighted concentration is calculated using a weight to reflect the previous concentration (this is done because the weighted C will be used for the Eulerian calculation and the processes of dispersion, source/sink mixing, and reactions occur throughout the time increment)
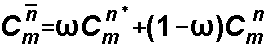
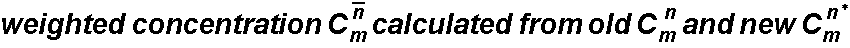
5. the weighted concentration is used to solve the second term (Eulerian portion) BEWARE! EXPLICIT, to avoid solving a large matrix limit the time step to:
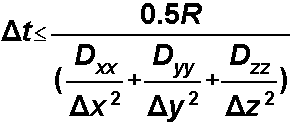
often the dispersive term is not the controlling factor due to advective constraints
6. the new concentration for cell m at time n+1 is:
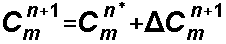
where:
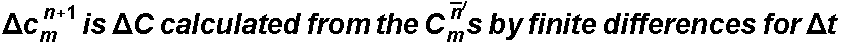
the concentration of each packet (l) is then updated, and depending on whether the concentration is increasing or decreasing, it is done differently
if the delta C due to dispersion is positive:
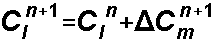
if the delta C due to dispersion is negative, to prevent negative concentrations:
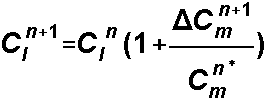
If no packets exist in a cell, the cell is assigned the concentration of the previous time step
7. repeat from step 1 until end of simulation - 2. packets are tracked forward using velocities based on head differences and K's and a small time step
Further discussion of the Method of Characteristics can be reviewed in Zheng and Bennett in Chapter 6, as well as in the MT3D manual by Zheng and Wang. The manual is available in the document sharing area of this course.
GO "BACK" TWICE to continue unit 13
OR GO "BACK" ONCE if you came from unit 14 and want to continue unit 14