Lecture:	9
Objective:	Understand the operation of the timer and how to use it to create precise delays.

Timer

The PIC timer subsystem is a sophisticated collection of circuitry to make precise time measurements. The core functionality of the timer, shown in the figure below, is the 16-bit counter. When enabled, the 16-bit counts up from 0 to 2¹⁶ - 1, and back to 0. The value of the counter is indirectly available through the 16-bit register TMR0, a variable that you can access in your C programs in the MPLab X integrated development environment.

The state of the timer, whether its running or stopped, is controlled by the TMR0ON bit in the Timer Control Register 0, called T0CON. Setting TMR0ON starts the timer counting up, clearing TMR0ON stops the timer. Like many of the bits in registers, MPLab X provides a convenient alias consisting of the register name and bit name concatenated with a "." character. So, for example, the following line of code starts the timer running.

	T0CONbits.TMR0ON = 1;

When the counter counts up from 2¹⁶-1 to 0, is is said to roll-over. This roll-over sets the TMR0IF bit in the INTCON register. This flag is sticky, meaning that once it's set by the 16-bit counter rolling over, it stays set until the user clears it in software. The TMR0IF bit is cleared by writing a 0 to that value. In other words, the following instruction clears the TMR0IF bit.

	INTCONbits.TMR0IF = 0;		// Clear timer overflow flag

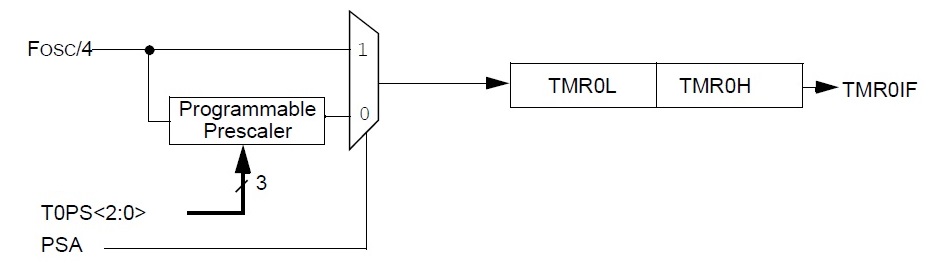
The timer subsystem, adapted from Figure 11-2 on page 161 of the PIC18F26K22 Data Sheet.

The timer counts up synchronously the main oscillator, F_osc, divided by 4. For the time being we will assume that the Programmable Prescaler is set to 1:1, meaning that it can be ignored. This means that on every fourth rising edge of the main oscillator, the counter counts up by 1. Since the PIC bus clock runs at 64MHz, the counter counts up at a rate of 16MHz. This means that in one second the timer counts up 16,000,000 times. Each of those counts takes:

	    1 second        62.5 ns
	----------------- = -------
	16,000,000 counts    count

This time interval, 62.5 ns, is the time resolution of the timer, meaning that we cannot confidently measure time intervals with an accuracy smaller than this value. This marks a good point to start measuring time with the timer using the following code snippet.

	T0CONbits.TMR0ON = 1;	// Assume that counter starts counting from 0
	INCONbits.TMR0IF = 0;	// Clear roll-over flag
	while(INTCONbits.TMR0IF == 0);	// Wait for roll-over flag to be set by counter

Your question is to calculate how long the while(INTCONbits.TMR0IF == 0); statement takes to execute, assuming that the counter starts at 0. In other words I am asking how long it takes for the counter to roll-over. The solution to this problem relies on dimensional analysis, the method of converting units of a quantity without changing its value. This relies on multiplying by a unity ratio, a ratio where the numerator and denominator are the same but represented in different terms. For example (60 seconds / 1 minute) is a unity ratio because both the numerator and denominator represent the same length of time. Dimensional analysis allows us to convert the bus clock into the time required to roll-over the timer.

     1 second      1000 ms     1 clk    2^16 counts 
    ------------ * -------- * ------- * ----------- 
    16*10^6 clks   1 second   1 count   1 roll-over 

which comes out to  4.10 ms
                   ---------
                   roll-over

Notice that the units clks, counts and seconds cancel each other leaving the units on the right. This is of fundamental importance to demonstrate on the exam. Do not skip any of the conversions, even "obvious" ones like converting seconds to milliseconds.

Just like how the time resolution sets a lower limit on the resolutions of time measurements, the value of 4.10 ms sets an upper bound on the time resolution of the 16-bit counter using a 1:1 prescaler. In order to measure time intervals longer than this, we will need to resort to other methods. One obvious method would be to put the delay loop inside a larger counting loop that iterated the 4.10 ms delay as many times as needed. Another method we will explore in the next lecture is to prescale the bus clock before it gets to the 16-bit counter, slowing down the rate at which the counter increments and thus increasing the amount of time it takes the counter to roll-over.

In general, when I am working one of these problems, I work through the equation from left to right, starting on the left with the bus clock. You can simplify your life by choosing the proper ratio for the bus clock. By this I mean, you have two choices for the bus clock, (1 second / 16*10^6 counts) or (16*10^6 counts / 1 second). Since the question asked for the time for a roll-over, I knew that we needed time units in the numerator. Thus, I choose the bus clock ratio with time units in the numerator.

Finally, note that this question was really asking for a unity ratio, the ratio of two representations of the same quantity expressed using different "rulers". The next question requires that we build a unity ratio and then multiply it by a constant to determine the solution. Calculate the number of timer counts that go by during 1 ms.

    16*10^6 clks   1 second   1 count  
    ------------ * -------- * ------- * 1 ms = x count
      1 second     1000 ms     1 clk

Solving for x yields x = 16,000

This problem is different, because you need to put information on both sides of the equation and some of the terms are not unity ratios.

Some problems

Question:How much time goes by in 30,00 counts? State your answer in ms and round to 3 significant figures.
Answer:

      1 second     1000 ms     1 clk    
    ------------ * -------- * ------- * 30,000 counts = 1.88ms
    16*10^6 clks   1 second   1 count

Question:Starting at 30,000, how long will it take TMR0 to roll-over? State your answer in ms and round to 3 significant figures.
Answer: There are 2¹⁶-30,000=35,536 counts until TMR0 rolls-over.

      1 second     1000 ms     1 clk    35,536 counts     2.22 ms
    ------------ * -------- * ------- * ------------- = ---------
    16*10^6 clks   1 second   1 count    roll over      roll over

Question:What starting value would result in TMR0 rolling over in 3ms?
Answer: We will call the tarting value of the TMR0, x. TRM0 has to count up from x to 2¹⁶ in order to roll-over. This is a total of 2^-x-x counts. This term is used int he solution to the problem.
```
      1 second     1000 ms     1 clk       2¹⁶-x  
    ------------ * -------- * ------- * ---------- = 3 ms
    16*10^6 clks   1 second   1 count    roll over      

solving for x yields, x = 17,536
```
Question:In the algorithm below, what initial value for TMR0 would produce a 2ms pulse on RA0?
```
	TMR0 = ______;
	INTCONbits.TMR0IF = 0;
	LATAbits.LAT0 = 1;
	while(INTCONbits.TMR0IF == 0);
	LATAbits.LAT0 = 0;
```
Answer: The calculation of the initial TMR0 for this code is the same as the calculation for the previous problem. We will call the target value of the TMR0, x. TRM0 has to count up from x to 2¹⁶ in order to roll-over. This is a total of 2^-x-x counts. This term is used in the solution to the problem.
```
      1 second     1000 ms     1 clk    2¹⁶-x  
    ------------ * -------- * ------- * ------------- = 2 ms
    16*10^6 clks   1 second   1 count    roll over      

Solving for x yields x = 33,536.
```
Question:An active low push button is connection to RA2, is pressed for an unknown amount of time - except that we know that it is not more than 4ms. Complete the program below to measure the number of TMR0 counts of the button press. would produce a 2ms pulse on RA0?
```
	while(PORTAbits.RA2 == ____);		// wait for press
	start = TMR0;
	while(PORTAbits.RA2 == ____);		// wait for release
	end = TMR0;
	duration =  __________;
```
Answer: The first delay loop must wait for the user to press the button, meaning that the code must wait while the button produces its nominal logic level. An active low push button is nominally logic 1, hence the first line reads: while(PORTAbits.RA2 == 1);

The second delay loop must wait for the user to release the button, meaning the code must wait while the button produces its active logi level. An active low push button produces a logic 0 when pressed, hence the third line reads: while(PORTAbits.RA2 == 0);

Since the time that the button press ends is greater than the starting time that the button is pressed, the difference of the end and start time is computed in the last line. duration = end - start; There is one very big caveat that we must address and that is what happens if TMR0 overflows between start and end? This situation is pictured in the figure below.

If the timer rolls over during the button press, then end < start. Since subtraction of end - start is equivalent to addition of end with the 2's complement start we can re-write duration = end - start; as duration = end + (2¹⁶ - start); The second term in this statement (2¹⁶ - start) is just the number of timer counts from the start of the button press until the timer rolls-over (the timer rolls over when it gets to 2¹⁶). This is illustrated as the red line on the right side of the number line above. The term "end" in the expression end + (2¹⁶ - start); is just the number of timer counts from 0. This is illustrated as the red line on the left side of the number line above. Thus the sum of these two number lines accuratly describes the number of timer counts the button was pressed.

Question:How many TMR0 counts occur in 1.5ms?
Answer:

    16*10^6 clks   1 second   1 count    
    ------------ * -------- * ------- * 1.5 ms = 24,000 counts
      1 second     1000 ms     1 clk

Question:How many times would TMR0 rollover in 100 seconds?
Answer:

    16*10^6 clks  1 count   1 rollover 
    ------------ *------- * ---------- * 100 s = 24,414 rollovers
      1 second     1 clk    2¹⁶ counts

Question:Starting at 0, what value would be stored in TMR0 after 10ms?
Answer: TMR0 will roll over because TMR0 only required 4.1ms (from earlier work) to roll over. So my first step in this problem is to compute how many times TMR0 rolls over.
```
    16*10^6 clks   1 second   1 count   1 rollover
    ------------ * -------- * ------- * ---------- * 10 ms = 2.44 rollovers
      1 second     1000 ms     1 clk    2¹⁶ counts
```
From this we know that TMR0 will count up from 0 to 2¹⁶-1 two times with 0.44 of a roll over left over. The second part of the problem will convert this 0.44 roll overs into counts.
```
    2¹⁶ counts 
    ---------- * 0.44 rollovers = 28,928 counts
    1 rollvers    
```
So, starting at 0, TMR0 will end up at 28,928.

The rate at which the timer counts up is primarily determined by the 16 MHz bus clock, but can be slowed down using a prescaler. This is a topic that we will take up next lecture.

Test your understanding

You can find the solutions embedded in the "source code" for this web page by right mouse clicking on this web page and selecting "view source". The solutions are in HTML comments.

Assume that the counter is currently at 0xABCD, how long will it take for the counter to roll-over. You should assume that the prescaler is 1:1. State your answer in milliseconds with 3 significant figures.
Assume that the counter is currently at 0xABCD, how long will it take for the counter to reach 0x1234. You should assume that the prescaler is 1:1. State your answer in milliseconds with 3 significant figures.
Assume that the counter is currently at 0 and that the prescaler is 1:1. What value will the counter have in 1.0 ms?
Assume that the counter is currently at 0 and that the prescaler is 1:1. What value will the counter have in 10.0 ms?
How many times will the counter roll-over when counting up from 0 with a 1:1 prescaler in 3.14 seconds?
The following questions assume that the counter is running a prescaler of 1:1.
1. Assume the timer starts counting at 0x0000, what will it read in 1mS?
2. Assume the timer starts counting at 0x0000, what will it read in 0.9375mS?
3. Assume the timer starts counting at 0x0000, what will it read in 1.875mS?
4. Assume the timer starts counting at 0x0000, how long does it take the counter to reach 0x1000?
5. Assume the timer starts counting at 0x0000, how long does it take the counter to roll over?
6. Assume the timer starts counting at 0xF000, how long does it take the counter to roll over?
7. Assume the timer starts counting at 0xF000, how long does it take the counter to reach 0x1000?