EENG 383
Lecture: 24
Objective: Design of a real LPF with standard components.

Analog to Digital Conversion

Passive Low Pass Filter

A passive low pass filter can be built from a resistor and capacitor arranged in the configuration shown below.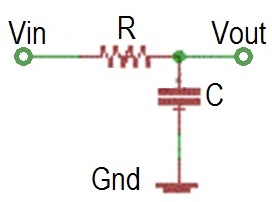


This is a first order filter with the following characteristics.

Active Low Pass Filter

The main drawback of a passive filter is that it loads the signal source with its impedance. An active filter decreases this burden and in most cases produces better results. Designing an active low pass filter can be a little overwhelming as their are a variety of topologies (arrangements of electronics circuit elements), filter types (Butterworth, Chebyshev, and Bessel to name a few), and op-amps. A complete study of these alternatives would be a course in itself, so you will have to be satisfied with this brief overview.
Probablly the most common active filter is shown below, a 2ond order Sallen-Key filter. Note that is has a pair RC elements, each serving the role of a single first order low-pass filter.


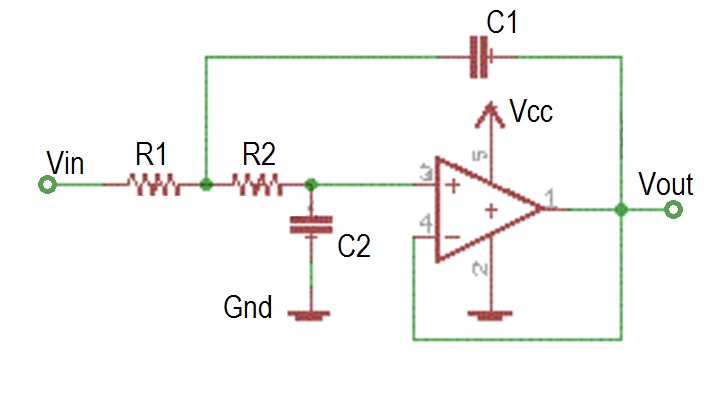
This filter does not have overwhelming performance, but makes up for that in its predictiable performance given in the following list. Frequently designers will set R1 = R2 and C1 = C2 with the effect of simplifying the design. Furthermore, if possible the resistance should be set between 1k and 10kΩ. This produces the following Bode plot.


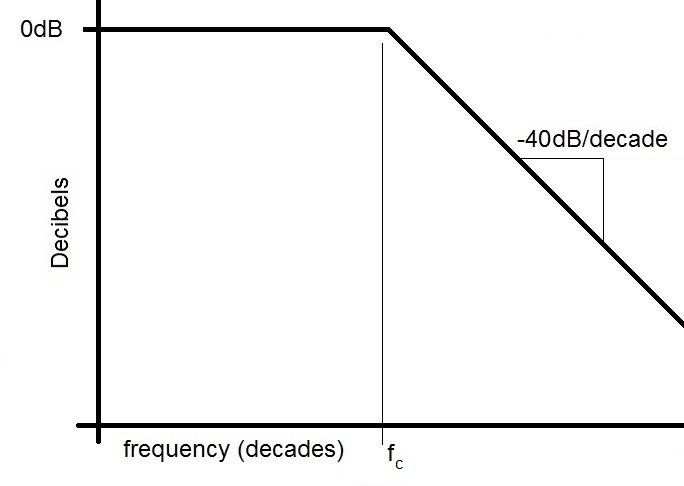
The choice of op-amps is not terriably important for modest applications with signals of interest below 1MHz.

E-series resistors

International standard IEC 60063 defines the preferred values for resistors and capacitors in a decade. "In a decade" means values with the same power of ten when written in scientific notation. The number of distinct values in any decade if defines the number after the "E" with 6,12,24,... being the standard for electronics. The intervals between values in a decade are separated geometrically, meaning that to get the next value in the E-6 series you multiply by a value, not add to that values. The E-6 series divides a decade into 6 parts, so the multiplicative constant is 101/6 because after multiplying a value x by this constant 6 times you will get 10*x This is the next decade. A well equipped lab will have an E-6 series from 10Ω up to 10 MΩ Note each value in the E-12 column is a factor of 101/12 times larger than the preceeding value.
E-6 value E-12 value
10 10
  12
15 15
  18
22 22
  27
33 33
  39
47 47
  56
68 68
  82
When confronted with the task of selecting a resistor and capacitors to build a low pass filter you should choose one of these standard values while keeping the resistor in the 1k - 1000k interval and a ceramic capacitor in the 10pF - 1uF decades. These values will not load the driving circuit, are available in temperature tolerant packages, and are readily available. Finally, in many applications it is not imparative that you get the corner frequency exactly correct; close is often good enough.

Problem:
Design a first order low pass filter with a corner frequency of 1000 Hz. Use only E-6 series components.

Solution:
fc = 1/(2*pi*RC) = 1000Hz
R*C = 1.6*10^-4  = 160*10^-6
Now we need to find an RC product close to 160. From the Test your understanding problem at the end of the lecture we have several choices I'll choose 33*47 which is as close as we can get to 160? Remember that we should be able to get these values in any decade between 10 and 10,000,000. So all I need to do is get close any factor of 10 to 160. So lets choose a 3.3kΩ resistor. Then 
R*C = 160*10^-6 with R = 3.3kΩ 
yields C = 48nF

Test your understanding

You can find the solutions embedded in the "source code" for this web page by right mouse clicking on this web page and selecting "view source". The solutions are in HTML comments.