INVERSE MODELS:

A NECESSARY NEXT STEP IN

GROUNDWATER MODELING

Eileen P. Poeter⁽¹⁾ and Mary C. Hill⁽²⁾

⁽¹⁾ Department of Geology and Geological Engineering, Colorado School of Mines, Golden, CO 80401
⁽²⁾Water Resources Division, U.S. Geological Survey, Box 25046, MS 413, Denver, CO 80225

Abstract

Inverse models using, for example, nonlinear least-squares regression, provide capabilities that help modelers take full advantage of the insight available from groundwater models. However, lack of information about the requirements and benefits of inverse models is an obstacle to their widespread use. This paper presents a simple ground-water flow problem to illustrate the requirements and benefits of the nonlinear least-squares regression method of inverse modeling and discusses how these attributes apply to field problems. The benefits of inverse modeling include 1) expedited determination of best fit parameter values; 2) quantification of the a) quality of calibration, b) data shortcomings and needs, and c) confidence limits on parameter estimates and predictions; and 3) identification of issues that are easily overlooked during non-automated calibration.

Introduction

Regulatory agencies increasingly insist that questions of prediction reliability be addressed in groundwater modeling projects and this is difficult to accomplish using only non-automated calibration procedures (the trial-and-error approach commonly utilized to calibrate models; Anderson and Woessner, 1992). Use of inverse models (such as nonlinear least-squares regression and associated statistics) facilitates assessment of prediction reliability because the results yield not only parameter estimates and heads and flows simulated for the stresses of interest, but also confidence intervals for both the estimated parameters and the heads and flows, which are convenient for conveying the reliability of the results to regulators. Sensitivities, parameter standard deviations and correlations, and prediction standard deviations can be used to help evaluate whether model parameter estimates and predictions are reliably calculated with the available data and what additional data could be most useful in improving the model.

This article discusses the use of one method, nonlinear least-squares regression with simple parameters as an introduction to inverse modeling. Other approaches to inverse modeling, such as those presented by Hoeksema and Kitanidis (1984), Xiang et al. (1993), and RamaRoa et al. (1995), share many of the same characteristics, but, to keep the discussion simple, only one method is presented here.

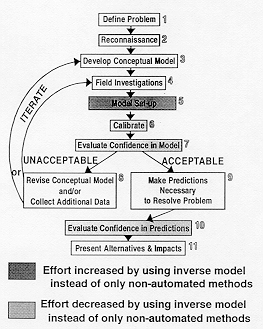
In essence, the process of calibration is the same using either inverse models or the non-automated approach: parameter values and other aspects of the model are adjusted until the dependent variables (heads and flows) match field observations. However use of an inverse model expedites the process of adjusting parameter values and provides additional results that offer numerous advantages in model analysis.

The fundamental benefit of inverse modeling is its ability to automatically calculate parameter values that produce the best fit between observed and simulated hydraulic heads and flows. Knowing that the parameter values are producing the best possible fit for a given conceptual model is crucial to the conclusive comparison of alternative models. If estimated parameter values for the best fit are outside of expected ranges, this is a vital clue about the validity of the conceptual model and the changes that might be needed. A calibration obtained via a non-automated approach alone is not optimized, hence moderate differences in "fit" cannot always be relied upon for selecting relative quality of conceptual models. Also, when a model is calibrated solely in the non-automated mode, numerous runs are spent changing parameter values and relatively few runs are spent adjusting the conceptual model. With inverse models used to determine parameter values that optimize the fit of the model results to the field observations for a given model configuration, the modeler is freed from tedious trial-and-error calibration involving changes in parameter values so more time can be spent addressing insightful questions about the hydrologic system. Less time is spent on questions such as "Which parameters should be changed and by how much?" and more time on more fundamental questions such as "What is it about the head observations and the boundary conditions that causes the best-fit estimated recharge to be one-tenth what I expect it to be?" or "What change could be made in the conceptual model to decrease the large differences between observed and simulated heads in the northern area of the model domain?" These types of issues are always present, but the tedium and uncertainty involved when parameter estimation is conducted by the non-automated approach often obscures them, making them difficult to address conclusively.

Another benefit is the quantification of 1) the quality of calibration, 2) data shortcomings and needs, and 3) confidence in estimates and predictions help communicate the results of modeling studies. Such quantifications are a natural result of inverse modeling for groundwater model calibration.

A third benefit is that inverse modeling reveals issues that even experienced modelers can easily overlook during non-automated calibration efforts. Extreme parameter correlation (e.g., parameters for which only the ratio and not their individual values can be determined) and lack of sensitivity of parameters to calibration data (i.e., the data do not provide enough information about a parameter) can be difficult to identify during non-automated calibration especially for complicated models. These are, however, clearly delineated in each automated calibration run. Effects of both available and anticipated data on the uncertainty and correlation of estimated parameters can be quantified through automated calibration. Consequently, the results can be used to design and guide data collection activities, as suggested by Knopman and Voss (1989).

Finally, automated calibration results are more amenable to use in quantitative comparison of alternative conceptual models, and use of automated methods encourages the consideration of these alternatives because the modeler does not spend as much time estimating the parameter values for each conceptual model. With the advent of practical nonlinear least-squares inverse software such as MODINV (Doherty, 1990), MODFLOWP (Hill, 1992), and PEST (Doherty, 1994) the use of automated methods for calibration and model analysis is more readily accomplished.

A major obstacle to widespread use of automated calibration by the practicing geohydrologist is lack of information about the requirements and benefits of automated calibration. First, there are no additional data requirements in order to undertake automated calibration. If you are ready to undertake a calibration project, then you are ready to include inverse modeling in that calibration. The objective of this paper is to disseminate information about automated calibration in order that the practicing geohydrologist will add a valuable tool to their study of groundwater flow. This presentation is facilitated through a simple model and associated graphics. Thorough discussion of the underlying assumptions and equations is provided by Hill (1994, 1992), Sun (1994), Helsel and Hirsch (1992), Cooley and Naff (1990), Seber and Wild (1989), and Draper and Smith (1982).

The MODFLOWP code (Hill, 1992) is used in this article. We use MODFLOWP for automated calibration of field problems because it: 1) can estimate many aspects of groundwater flow systems, such as transmissivity, conductance of stream and lake beds, recharge rates, flow at specified flux boundaries, head at specified head boundaries, and many other values; 2) can represent complicated parameter definitions using interpolation methods such as kriging for spatially distributed parameters (e.g., hydraulic conductivity) allowing use of, for example, the pilot points method (RamaRoa et al., 1995); 3) utilizes many types of observations such as flow rates, hydraulic heads, and temporal changes in head, as well as prior, or direct, information on parameter values; 4) provides extensive sensitivity analysis and statistics that allow the modeler to evaluate results; 5) uses sensitivities calculated by the accurate sensitivity-equation method; 6) is based on the widely used three-dimensional, transient, groundwater flow code MODFLOW (McDonald and Harbaugh, 1988; Prudic, 1989; Hill, 1990); and 7) is public domain, so it is inexpensive. Although this article utilizes MODFLOWP to provide illustrative examples, the major characteristics described and conclusions drawn concerning automated calibration are independent of the modeling code, and are applicable outside the field of groundwater hydrology.

Parameter estimation using inverse modeling

A flow chart of a geohydrologic project is presented as Figure 1. If the model used for the project is a numerical simulator, then steps 6, 7, and 10 are expensive and time consuming. The cost of these steps can be reduced and the quality of the outcome improved by using inverse modeling to estimate parameters. Compared to non-automated calibration, more effort is expended in step five because additional input is required for inverse modeling. Instead of entering only model geometry, material properties, and boundary conditions, as is required in non-automated calibration, the modeler also enters the data used for calibration, i.e., the parameter definition, field observations (for example, measurements of hydraulic heads and flows), independently derived values of the parameters (generally called prior information), and variances of the measured hydraulic heads, flows, and parameters. The variances are used to calculate weights, which are discussed later.

Figure 1. Flow chart of a hydrogeologic project.

After execution of a model with initial estimates of parameter values, an automated calibration code: 1) determines the differences (residuals) between observed and simulated values of heads, flows, and parameters, at all locations and times in the model; 2) squares the residuals to eliminate negative values and emphasize the larger residuals; 3) weights the importance of each squared residual by the amount of uncertainty the modeler specifies for each observation, as expressed by the inverse of observation error variances; 4) sums the weighted residuals to obtain an overall measure (an objective function) of how well the field observations match the model simulated values ("goodness of fit"); 5) calculates sensitivities (i.e., how much the simulated heads and/or flows would change given a change in the parameter values); and 6) uses the sensitivities and residuals to adjust the parameter values to minimize the objective function.

An automated calibration can be used only to estimate specific parameters as selected by the modeler --- all other aspects of the model are still calibrated by a non-automated procedure. However, because the majority of computer runs on a non-automated calibration are usually spent estimating parameter values, inverse modeling is extremely useful.

Introduction of the example problem

The example problem used in this article is simple enough that every aspect of it can be understood through geohydrologic reasoning and calculated analytically. Experience has shown that the concepts presented using the example problem are extremely useful for complicated field problems as discussed below. The example problem used here is similar to one of the problems presented by Carerra and Neuman (1986). An overall gradient of 9x10^-3 (a head of 10m and 1m on the west and east respectively) is imposed between no-flow boundaries (north and south) of a confined system (450m wide and 999m long) with a zone of low transmissivity (0.1 m²/s) separating two zones of high transmissivity (1.0 m²/s), Figure 2a.

Figure 2. Sample problem configuration, head observations, and contour plot and 2 1/2 dimensional rendering of the log of the sum-of-squared residuals surface. The cross indicates the true values of transmissivity.

Sum-of-squared residual surfaces are used in this article to display the characteristics of the calibration problem. For this simple problem, with six head observations measured with perfect accuracy ("true heads"), the sum-of-squared residuals surface for two parameters is illustrated in Figure 2b. A sum-of-squared residuals surface can be generated by simulation using different sets of parameter values as follows: calculate the sum-of-squared residuals for each set, plot them on a graph with axes representing the parameter values, and contour the sum-of-squared residuals.

The ratio of the number of observations to the number of estimated parameters in this problem is 6/2=3. In most applications this ratio would be larger; a limited number of observations is used here for clarity.

Parameter correlation

Correlation can be calculated between any pair of estimated parameters using standard linear methods (Draper and Smith, 1981, p.111) and can range between -1.0 and +1.0. Absolute values near one indicate that coordinated linear changes in parameter values would produce the same heads and flows at the observation locations; smaller absolute values indicate that no such coordinated linear changes exist. Correlation coefficients are calculated by inverting a matrix which is singular when correlations are -1.0 or +1.0. Singularity generally prohibits inverting a matrix but it can be accomplished in the presence of round-off error, as in this work.

The sum-of-squared residuals surface of Figure 2b exhibits minimum values along a trough, indicating that the two transmissivities have a correlation of one. Any two transmissivities with the same ratio as the true transmissivities (T1:T2 = 10:1) will yield the same head distribution and, therefore, the same minimum sum-of-squared residuals value if only head observations are included in the regression. Combinations of T1 and T2 that differ from 10:1 result in a larger sum-of-squared residuals value. Ratios less than 10:1 (the lower right section of the graph) have larger sum-of-squared residuals values than ratios greater than 10:1 (upper left section) because, not only are the relative values incorrect, but, for ratios less than 1:1, the position of high and low transmissivity materials is reversed. When the parameters are extremely correlated, as are T1 and T2 using only head observations, the final estimated parameter values depend on the starting parameter values. In this test case, starting values of T1=0.9 and T2=0.2 led to optimized values of T1=0.56 and T2=0.056; while starting values of T1=1000 and T2=1000 led to optimized values of T1=27.3 and T2=2.73.

Extreme correlation of parameters is common in groundwater modeling because observations required to uniquely determine parameter values are frequently lacking. Such correlation is sometimes recognized when using non-automated calibration methods, but is always revealed when inverse methods are used properly. This is especially important for complicated systems in which extreme correlations are more difficult to identify without inverse models. Once extreme correlation between estimated parameters is recognized, the modeler can either choose to set one or more of the parameters to specified values and estimate the others (again, only the ratio of the parameters is determined and the estimated parameter values are only as accurate as the specified parameter values), or collect additional data that will uniquely define all parameter values.

Decreasing parameter correlation and consideration of nonlinearity

Decreasing parameter correlation from 1.0 to 0.98 is typically enough to individually estimate the parameter values, as indicated by a single minimum being obtained from several sets of starting values. Flow observations (e.g., groundwater discharge along a stream reach) generally decrease the correlation between parameters that is present in cases where only head observations are available. In the example problem, a distinct minimum exists in the sum-of-squared residuals surface when the flow leaving the system is added as an observation (Figure 3). In this case, in which all the flow leaving the system is measured, unique parameter estimates can be obtained.

Figure 3. Sample problem including a flow oservation q. The minimum is -11 (the log of values near zero).

The complete sum-of-squared residuals surface usually is not calculated and displayed by inverse models because it would require many unnecessary calculations. Also, normally more than two parameters are estimated, making complete display difficult or impossible. Accordingly, the modeler must use calculated parameter correlations rather than a graphical image.

Calculated parameter correlations depend on the parameter values because the inverse problem for ground-water flow is nonlinear with respect to most parameters of interest -- that is, hydraulic heads and flows are not a linear function of the estimated parameters, so that sensitivities are different for different parameter values. This nonlinearity is sometimes a confusing concept for ground-water hydrologists because they are used to thinking of the ground-water flow equation as linear when applied to confined layers, a characteristic which allows application of the principle of superposition. That is, however, linearity of the differential equation that relates hydraulic head to space and time given fixed parameters values, not linearity of hydraulic head with respect to parameters. In a confined aquifer, doubling the pumping rate doubles drawdown, all else being the same, but if the subsurface material changed from coarse to fine, all else being the same, there would not be a linear relation between the change in drawdown and the change in hydraulic conductivity. If the regression problem presented in Figure 3 was linear, the contours of the sum-of-squared residuals surface would be elliptic. The sum-of-squared residuals surface of this sample problem is exceptionally non-elliptic; many groundwater problems exhibit a more elliptic and concave surface as opposed to the odd shape and convex ridge exhibited in Figure 3. Nonlinearity of the inverse problem is discussed more fully by Hill (1992, pp. 69-70).

When the flow observation is included in the regression (using an appropriate weight as discussed later), the correlation calculated for the true values of T1 and T2 is 0.86, compared to 1.0 for all sets of parameter values without the flow observation. To illustrate the effect of nonlinearity with respect to the parameters, correlations between T1 and T2 at selected parameter values are presented in Figure 4. The absolute values of the correlations range between 0.05 and 0.998, with larger values along the 10:1 ratio line. This amount of variation is exceptional, and is indicative of the extreme nonlinearity of this problem and the three order-of-magnitude variation in parameter values considered. Yet, even in this extremely nonlinear problem, the correlations provide useful information to the modeler. Nearly all values clearly demonstrate that the flow data diminishes the complete correlation between the parameters and, therefore, provides information from which the parameters can be estimated individually.

Figure 4. Correlation of T1 and T2 at specified parameter values.

An important characteristic of the calculated correlations is that only the sensitivities are used in their calculation; they are independent of the value of the observation. Consequently, in the example problem, the correlations could have been calculated before measuring the flow to determine whether inclusion of the measurement would reduce correlation.

Although obvious in this simple test case, problems of correlation and identification of the data needed to diminish the correlation often go unnoticed in complex problems encountered during practical application of groundwater modeling. In such problems, there are generally more than two parameters, and correlation coefficients are calculated for each possible pair of parameters.

Although not illustrated in the example problem, independently measured values of the parameters (e.g., transmissivities from aquifer tests) can be used to decrease correlation, and this often is useful in complex problems. In such a case, the objective function includes not only the difference between observed and simulated heads and flows but also the difference between observed and estimated parameter values.

Observation errors, weighting, and the calculated error variance

In Figures 2 and 3, the sum-of-squared residuals value equals zero at the minimum of the surface. This is because the observations are error-free, and the model is a perfect representation of the system. Field observations include error, and model representations are never a perfect reflection of field conditions, thus the minimum sum-of-squared residuals value always is larger than zero in field applications. The surface illustrated in Figure 5 is calculated using observations with errors as indicated on the figure and has a similar shape to the one presented in Figure 3, but, overall, the sum-of-squared residuals values are of greater magnitude and the minimum is higher.

Figure 5. Sample problem using observations with errors with two iteration paths followed by MODFLOP. The minimum is -0.2.

Errors associated with field observations are caused by inaccuracy and imprecision of the measuring device or observation process, and by human error. Errors also result because the computer model is a simplification of the physical system. For example, if the head observed in a well is a perfect measurement, a difference between observed and simulated head may result because the simulated head represents the average head over a volume of material with average properties. If the observation is not at a nodal point in the computer model, the nodal values are interpolated to obtain the simulated value for comparison. This is illustrated in Figure 6, which is drawn with large discretization to exaggerate the problem. This is one of many possible model errors. Comprehensive discussion of these errors is beyond the scope of this presentation, further discussion is provided by Anderson and Woessner (1992) and Hill (1992).

Figure 6. Schematic of exaggerated difference between physical and numerical systems illustrating model error.

To use nonlinear regression, the modeler needs to assign variances (or standard deviations or coefficients of variation that are used to calculate variances) to all observations. The variances can reflect estimated measurement error and, sometimes, model error.⁽³⁾ For example, if the modeler estimates that there is a 95% probability that the true head is within +/-0.5m of the observed head and that a normal probability distribution applies, then a normal probability distribution table can be used to determine that +/-0.5m is 1.96 standard deviations. Consequently, 1.96 = 0.5m and the standard deviation, , is 0.26m. The variance is the square of the standard deviation (²), or 0.066m². Each squared residual is weighted by the inverse of the variance (weight = 1/²) before the sum-of-squared residuals value is calculated, so observations which the modeler regards as less prone to error (smaller variance) have more importance in determining the parameter values. For example, a modeler will assign less weight (higher variance) to a head observation for which casing elevation is estimated from a topographic map as opposed to an elevation measured by precise surveying from a benchmark. The squared residuals have units of (L)² for heads or (L³T^-1)² for flows and the respective weights have units of (L)^-2 or (L³T^-1)^-2 so the weighted squared residuals are dimensionless when summed. A residual times the square root of its weight is called a weighted residual. For the sample problem presented herein, heads are assigned a variance of 0.005m² and the flow observation is assigned a variance of 0.03(m³/s)² (approximately equivalent to a 95% probability that the true head is within +/-0.14m and the true flow is within +/-0.34m³/s). Although assignment of weights is subjective, it is reassuring to note that, in most circumstances, the estimated parameter values and calculated statistics are not very sensitive to moderate changes in the weights used.

An accurate model tends to have weighted residuals that are randomly distributed in space and time, so that they do not display consistent spatial or temporal trends. For example, the validity of a calibrated model would be doubted if all the simulated heads in a given layer were higher than the measured heads. This is similar to analyses commonly used when calibration is accomplished with only non-automated methods.

The calculated error variance is a statistic that can be used to reveal how well the simulated values match the observations relative to their assigned weighting. The calculated error variance equals the sum-of-squared weighted residuals divided by the difference between the number of observations and the number of parameters (e.g., 10^-0.2/(7-2)=0.13 at the minimum of the objective function surface for the case using both head and flow observations with error). A statistic called the standard error of the regression is the square root of the calculated error variance (0.36 for the case with a flow observation). If, overall, the model fits the observations in a way that is consistent with the assigned weighting, the calculated error variance and the standard error of the regression will equal about 1.0. Smaller values indicate that the model fits the observations better than was indicated by the assigned weighting: the standard error of 0.36 in the above example indicates that the model fit the observations better by a factor of about 0.36 than the assigned variances indicated. Values of the calculated error variance and the standard error that are larger than 1.0 indicate that the model fit is not as good as indicated by the assigned weighting. Values larger than 1.0 are common in practice because the assigned weighting usually reflects expected measurement error, while the weighted residuals are also affected by model error. However, as mentioned previously, the presence of model error does not necessarily indicate a poor model or an invalid regression if the weighted residuals are random.

The method of assigning weights described above was developed by Hill et al. (in review) and is a variation of the method commonly described in the literature (Carrera and Neuman, 1986; Cooley and Naff, 1990), but is easier to apply when multiple types of observations are used.

Selection of parameter values by an inverse model

To estimate the parameter values, MODFLOWP starts at a user-defined set of parameter values and calculates the sensitivity of the simulated value at each observation point for each parameter being estimated. The sensitivities are used with the residuals to determine the magnitude and direction (+/-) of parameter adjustments needed to decrease the sum of the weighted, squared differences between observed and simulated values. All parameters are adjusted simultaneously.

For the situation presented in Figure 5, and starting with values of 1000 m²/s for both T1 and T2 (i.e., 3 in log space), the starting sum-of-squared residuals value is greater than 1x10⁷. Using the sensitivities and the weighted residuals, regression results indicate that the next estimates of T1 and T2 must be smaller and T2 must be adjusted by a larger increment. A maximum percent change of parameter value can be specified to limit parameter adjustments, thus preventing oscillations and overshooting. The mathematics used to adjust parameters are described by Hill (1992).

Although it is likely that this second set of calculated hydraulic heads and flows fit the observed values better, it probably will not be the best fit. Consequently, the modified parameter values are used to run the model again. The code again evaluates the sensitivities (because of the nonlinearities, these will be different than the sensitivities calculated before), estimates a new set of parameters, executes the model and calculates the difference between observed and simulated values. This process is repeated again and again, generally decreasing the sum-of-squared residuals by steps as shown in Figure 5.

Due to the errors inherent in the observed values and the imperfection caused by representing the groundwater system with a simple and discrete mathematical model, the sum of the squared differences will not be zero for any combination of parameter values. Accordingly, the code terminates this iterative process (i.e. converges) when the parameters change less than a percent specified by the modeler.

Even with error in the observations and starting values much different than the true values (1000 m²s for T1 and T2), the sample problem is well behaved if both head and flow observations are utilized. In this situation MODFLOWP followed the parameter iteration path in the upper right quadrant of Figure 5 and converged on parameter values of 0.94 and 0.094 m²/s (10:1) for T1 and T2 respectively. This combination of T1 and T2 yields an outflow of -0.95 m³s, precisely the error-burdened value of flow input as an observation. This precise match is typical when one observation reduces what would otherwise be very high correlation. The shape of the objective function surface is the result of the nonlinearity discussed earlier and makes the regression difficult, thus more iterations than usual are required to find the minimum when starting values are far from the minimum. Typically the number of iterations required for convergence is less than twice the number of estimated parameters.

For a few problems, the sum-of-squared residuals surface may exhibit local minima (Bevin and Binley, 1992, p. 291; Carrera and Neuman, 1986, p. 215). Generally, modelers want to find the lowest point on the surface (the global minimum). To ensure that the minimum reached is a global minimum, it is suggested that the model be run more than once, using different sets of starting values. Figure 5 shows that starting the regression from T1, T2 equal to 1000,1000m²/s and equal to 10,0.001m²/s yields the same minimum.

There are a number of issues to consider with regard to the use of automated calibration, such as: coping with sparse data when there are many parameters to estimate; using results for designing data collection; appropriate procedures when estimated parameter values are unreasonable; determining the confidence in the modeling results; and evaluating alternative conceptual models. These issues are discussed in the following sections.

When there are many parameters to estimate and not many observations

It may not be reasonable to estimate every parameter of interest with the available data. It is obvious that we cannot solve for more unknowns than we have equations. Similarly we do not estimate more parameters than we have observations. In fact, the observations we obtain from the field are redundant. Accordingly, to make reasonable parameter estimations, we estimate substantially fewer parameters than the number of observations so that the data are not "spread too thin." This condition is true regardless of how parameters are estimated, but automated calibration methods can be used to clearly reveal the problem so that it can be addressed directly by the modeler.

Two resolutions are possible: estimate fewer parameters or collect more data. The first suggestion is often discounted, however, applied judiciously, much of the relevant physics can be represented by a model with relatively few parameters. This limitation is not caused by some arbitrary criterion, but by the lack of information contained in the data that are available for calibration. This problem is present in all calibration; inverse models simply make the problem more obvious.

Judiciously defining parameters for estimation requires the ability to distribute parameters in a manner consistent with knowledge of the subsurface material. If units are known to have nearly homogeneous hydraulic conductivities, zonation methods can be used to apply a single parameter value to the entire unit. If geohydrologic knowledge suggests that hydraulic conductivity varies smoothly in a two- or three-dimensional region of the subsurface, the user needs to be able to use interpolation methods. Most commonly, interpolation methods are used to distribute the influence of hydraulic conductivities estimated at individual points. The pilot points method (RamaRoa and others, 1995) is an example of this approach; others are suggested by Yoon and Yeh (1976), Keidser and Rosbjerg (1991), and Hill and others (in review). Consequently, automated calibration codes need to support a variety of methods of parameter distribution.

Inverse modeling makes the need to reduce the number of estimated parameters more obvious and provides information to guide the user in the reduction process. Automated calibration results 1) commonly reveal the character of the problem; 2) can be used to determine whether the parameters originally thought to be more important, are actually important to the simulation of the predictions of interest; and 3) can be used to determine what data are needed to estimate these parameters as discussed in the following section. In some circumstances, it may not be possible to estimate all parameters simultaneously at first. A method that is sometimes useful is to first estimate the most sensitive parameters, then, using the optimized values for these first parameters as initial values, estimate the entire set of parameters (Hill, 1992, Appendix B; Yager, 1993).

Inverse modeling as a guide to data collection

Calculated parameter sensitivities and their associated statistics can be used to guide data collection activities because they indicate: 1) whether available (or new) data are likely to adequately estimate the parameter values; 2) where additional data probably would be most useful in improving the estimated parameter values; and 3) the likely effect of new data on the certainty of simulated heads and flows.

Sensitivities calculated for the example problem are zero at the midpoint of the system, as shown in Figure 7. These sensitivities indicate that collection of a head observation at this location would be of no value. We know this intuitively because the heads in a symmetric system with a head specified on each end will simply pivot around the same value of head at the midpoint when the transmissivities are varied. An observation at such a point would not help the parameter estimation unless it causes the modeler to alter the conceptual model (e.g., to define asymmetric conditions). Sensitivity is also low near the boundaries because the constant heads prevent the simulated head from changing significantly for different parameter values. If the modeler is uncertain of the head at the boundary, it can be estimated and, in such a case, sensitivity of the estimated head to heads measured near the boundary would be large, but sensitivity to the transmissivities would not change. Given the model geometry and boundary conditions, the most valuable head data for estimating transmissivities lie near the material property boundaries. Consideration of the underlying cause of both the high and low sensitivities can enhance geohydrologic insight and help to determine the next activity for the project.

Figure 7. Sensitivity of observations to changes in values of parameters T1 and T2 at the true parameter values (1.0 and 0.1 m²/s respectively).

The sensitivities of the flow observation, q, to log T1 and log T2 shown in Figure 7 are negative, indicating that if either T1 or T2 decrease, q increases. An increase in outflow is actually a decrease in the volumetric flow rate out of the model because outflow is negative (e.g., a change in outflow from -1.0 to -0.9 m³/s is a +0.1 increase). Similarly when T1 decreases, heads decrease on the left side of the model and increase on the right (Figure 8). The relation between head and T1 on the left yields positive sensitivities and the relation on the right yields negative sensitivities (Figure 7).

Figure 8. Head distribution for increased and decreased values of T1.

The sum-of-squared scaled sensitivities for each parameter represents composite scaled sensitivity of the observations (scaling is accomplished by multiplying the sensitivity by the parameter value and the square root of the weight). For example, the values of composite scaled sensitivity calculated for the estimated parameter values for the case including the flow observation are 0.24 for T1 and 3.9 for T2 for values of T1 and T2 equal to 0.9 and 0.2 respectively, and they are 4x10^-4 for T1 and 3.7 for T2 for the true values of T1 and T2, indicating that there is greater sensitivity to the lower transmissivity value.

The nonlinearity of the problem and the scaling used produce different values of composite sensitivity for different parameter values, but for many problems they are still useful. For example, see Anderman et al., in press, and D'Agnese et al., in review. If the composite scaled sensitivity is several orders of magnitude lower for one parameter, then the data probably do not provide much information about that parameter value and the regression may not be successful. As with correlation of parameters, if there is a problem, the modeler must either specify the value or add data to increase the sensitivity. Such a problem may go unnoticed in a non-automated calibration.

When the estimated parameter values are not reasonable

Parameter values estimated by automated calibration may be implausibly large or small, and in some cases, relative magnitudes are reversed. For example, estimated hydraulic conductivity of an unconsolidated gravel may be less than the estimated hydraulic conductivity of a silt. In addressing this problem, it is important to note that 1) the automated calibration is simply determining the parameter values that produce the best model fit with the observations, and 2) if the model is correct and the observations represent what we think they represent, we expect the best-fit parameters to be reasonable. Unreasonable estimates for parameters with substantial composite sensitivities, therefore, suggest that there is something about the model set up and(or) the observations (or, rarely, the weighting of the observations) that is producing the unreasonable parameter values. The most likely problem is that the model does not accurately represent some aspect of the physical system that is important with respect to the calibration data. The modeler then needs to closely reconsider model construction. Another possibility is that there may be problems with some of the observations. Hints can be derived from evaluation of the residuals. Questions that might be considered include, for example, "Does the model need to be three-dimensional instead of two-dimensional?", "Are the residuals in the northern part of the lower layer all positive because a continuous confining bed of uniform vertical hydraulic conductivity is assumed and it might not be continuous or uniform?" Such questioning can produce insightful analysis of the physical system, and is generally more challenging and productive than the questions about what would take place if parameter values were changed by some amount, which is common when parameter values are estimated by non-automated calibration.

Some users may wish to impose reasonable parameter values despite the tendency of an automated calibration to estimate unreasonable values, but Hill et al. (in review) show that, if the observations contain a substantial amount of information about the parameter(s) in question, as indicated by confidence intervals (see following section) that do not include reasonable values, imposition of reasonable parameter values can produce less accurate predictions because the underlying model inaccuracies have not been addressed.

Determining the confidence with which the parameters are estimated

The first issue of interest after obtaining parameter estimates is determining the confidence with which the parameters are estimated. Confidence intervals are useful for this purpose, and can be approximated using first-order methods. The individual confidence intervals presented in this work are calculated as the final estimated parameter value +/- the product of the standard deviation of that estimate and the student-t statistic. The student-t statistic is dependent on the degrees-of-freedom of the problem (number of observations minus the number of parameters) and the desired level of confidence. The standard deviation is the product of the calculated error variance and a function of the weighted sensitivities. Confidence intervals are broad when a large change in a parameter value results in a small change in the sum-of-squared residuals as takes place if sensitivities are low, but the presence of parameter correlation can produce misleading results. For example, with six precise head observations, T1 is estimated precisely enough that the 95-percent confidence interval is (0.14;2.3) -- that is, the probability that the true value of T1 lies between 0.14 and 2.3 m²/s is greater than 95% (Figure 9). This is misleading because T1 and T2 are completely correlated if only head data are used and the modeler must be wary of such situations because the estimates are dependent on the starting values. For this simulation, the starting values were 0.9 and 0.2 m²/s for T1 and T2, respectively. Starting values of 1000 m²s^-1 for T1 and T2 yield parameter estimates of 27.3 and 2.73 m²/s with a 95 percent confidence interval on T1 of (10;74.2). With high parameter correlation, convergence on the proper ratio of parameters is obtained, but the calculated confidence intervals do not reflect the infinite range of possibilities.

Figure 9. 95% confidence intervals on parameters for cases utilizing only heads (h) and heads and and flows (h & q) for true observation values and observations with errors.

When an accurate, noiseless flow observation is added (Figure 3), T1 is estimated precisely enough that the probability that T1 lies between 0.9998 and 1.0007 m²/s is greater than 95% (Figure 9). The estimated values are accurate because the parameters are not highly correlated. Figure 9 reveals that accurate estimates (i.e., the true value falls within the confidence intervals) are obtained with both head and flow observations even if error is associated with their measurement. The estimates are more precise (i.e., narrower confidence intervals) if both heads and flows are used as observations or if errors are smaller.

The calculated error variance used when calculating the confidence intervals accounts for overall error in weighting of the residuals. As discussed previously, if the calculated error variance is greater than 1.0, this means that the model fit achieved by the calibration is not as good as would be consistent with the assigned weights. As long as the weighted residuals do not show any bias, however, the inclusion of the calculated error variance in the calculation of confidence intervals accommodates errors in the assigned weighting.

Determining the confidence with which hydraulic heads and flows are simulated using the estimated parameter values

Parameter standard deviations and correlation can be used to calculate confidence intervals on the values of heads and flows (or changes in heads and flows) simulated using those parameter values. These confidence intervals reflect how the uncertainty of the parameter estimates is propagated to the simulated heads and flows; no other source of uncertainty is included, thus they can be presented as the smallest possible range of prediction uncertainty. To illustrate, a well pumping 0.3 m³s^-1 (600 GPM) is included in the model (Figure 10). Assume that the head (or drawdown) at a specified location (X) and the flow rate (or depletion) of the outflow to the right boundary (q) are of concern. Since two criteria are considered, simultaneous confidence intervals are calculated, in contrast to individual confidence intervals presented above. The simultaneous confidence intervals are at least as broad as, and generally broader than, the 95% confidence interval on either simulated value considered individually. By using simultaneous confidence intervals, the modeler can make statements such as: With the available data (one flow and six head observations with error), the parameters are estimated precisely enough that the probability that the true head at "X" lies between 1.3 and 1.6, and the true flow at the boundary lies between -1.3 and -0.06 is greater than 95% (Figure 11). The simultaneous confidence intervals are calculated using the Bonferroni method (Hill, 1994, p. 29). Figure 11 shows that the precise observations yield simulated values with essentially no uncertainty for this well constrained problem, while observations with error yield larger intervals. If only the change in head or flow with and without pumping is of interest, the confidence intervals are smaller because uncertainty associated with determining the absolute value of head and flow is no longer included (Hill, 1994, p. 36-37).

Figure 10. Sample problem configuration with pumping well and points of concern.

Figure 11. Simultaneous 95% confidence intervals for head at x and flow at the right boundary, q.

Assumptions for calculating confidence intervals

When first order (also called linear) confidence intervals are calculated, it is assumed that 1) the true errors are normally distributed, 2) the model is approximately linear with respect to the parameters near the estimated values, and 3) the model correctly represents the relevant features of the system (so the uncertainty is only due to the uncertainty associated with the parameter estimates) (Seber and Wild, 1989).

It is not possible to determine whether the errors in field observations are normally distributed. Instead, the true errors are assumed to be normally distributed if the residuals are normally distributed. The linearity of the model in the vicinity of the estimated values can be analyzed using the programs presented by Cooley and Naff (1990) and Hill (1994). As the model deviates from normally distributed errors and linearity near the parameter values, the accuracy of the calculated confidence intervals declines. This is not a drawback to the use of automated calibration codes in relation to non-automated calibration because use of a non-automated approach does not improve the situation. It is unreasonable to even try to calculate confidence intervals using non-automated calibration methods

Inaccuracies due to nonlinearity are discussed by Donaldson and Schnabel (1987) and Christiansen and Cooley (in review). Nonlinear methods for calculating confidence intervals have been developed for groundwater flow problems (Vechia and Cooley, 1987), but are not presented in this work. They are much more computationally intensive than first order methods, but are needed in some cases.

Evaluation of the third assumption is best addressed by the user evaluating alternative conceptual models of the site. Evaluating statistics indicative of model fit, the confidence with which the parameters are estimated, and plotting weighted residuals as suggested by Cooley and Naff (1990) and Hill (1992) may be helpful in developing alternative models.

Using inverse modeling to evaluate alternative conceptual models

Alternative conceptual model evaluation is the most important aspect of groundwater modeling. It is often shortchanged in non-automated calibration because it is so time consuming to estimate parameter values for what is considered to be the most likely conceptual model, and each alternative conceptual model also must be calibrated to obtain the best-fit parameter values. As a result, alternative conceptual models are not typically tested. The results of an inverse model can be used to compare alternative conceptual models and quantify which models are more likely to be an accurate representation of the field based on the available data. For example, using the same set of observations, a conceptual model that is more likely an accurate model of the site would 1) exhibit no consistent spatial or temporal pattern in the weighted residuals; 2) result in more realistic estimated parameter values; and 3) have a smaller sum-of-squared residuals value in conjunction with narrower confidence intervals on the estimated parameters. A variety of statistics have been suggested for criteria three; see Carrera and Neuman (1986). If alternative conceptual models are subjected to automated calibration and none are clearly superior based on the above criteria, then they are equally likely alternatives given the available data. If no additional characterization is planned, then the desired predictions must be made for all the alternative models and decisions/plans can be based on the outcome of the modeling studies. If the alternative conceptual models and their estimated parameters yield such substantially different results for the prediction of interest that a reasonable decision is untenable, then additional data should be collected to eliminate the less accurate conceptual models.

To illustrate this concept, alternative conceptual models of the example problem are presented (Figure 12). Model 0 and 1 possess the correct model configuration with head observations only, and with head and flow observations, respectively. Models 2 through 7 all utilize both head and flow observations. Models 2 through 4 represent various possible configurations of the geohydrologic units. Models 5 through 7 have the true geohydrologic units configuration with differing boundary conditions. Model 5 includes recharge in the form of leakage to the top of the aquifer, and the value of recharge is estimated as a parameter. In model 6 the left boundary is inappropriately defined as 10.5 m rather than 10m. For model 7 recharge is included, but not estimated, rather it is specified at a value of 1x10^-5m/s.

Figure 12. Alternative conceptual models for the sample problem.

Models that are most similar to the true condition (models 1, 3, and 5) yield the lowest optimized sum-of-squared residual values (6 for models 1, 3, and 5; 101, 58, 74, and 767 for models 2, 4, 6, and 7 respectively) and the most accurate (near the true value) and precise (narrow confidence interval) parameter estimates, simulated values, and change in simulated values (Figure 13). Model 1 is, of course, the "true" model. Model 3 is a good representation because it is a nearly perfect replica of the system with only a minor variation in the geometry of the geohydrologic units. Model 5 is a good representation of the system because the recharge estimate is essentially zero (the 95% confidence interval on recharge straddles zero with an upper bound below 1x10^-6 m/s), and given a zero recharge model 5 is identical to the "true" system. The modeler can use such results to justify conceptual model selection. Results such as these can be used to defend the need to either evaluate the problem for the entire group of conceptual models or conduct field studies to eliminate some of the models.

Figure 13. Comparison of confidence intervals for 7 alternative conceptual models. An asterisk (*) indicates models most similar to the true conditions.

Extension of concepts to field problems

The concepts presented in this paper extend directly to field application, as indicated by the following publications: Tiedeman and Gorelick (1992); Yager (1993); Giacinto (1994); Olsthoorn (1995); Poeter and McKenna (1995); Anderman et al. (1996); D'Agnese et al. (in review) and references cited by Hill (1992). The broad applicability of the methods suggested here is demonstrated in the calibration of a three-dimensional advective-dispersive transport problem by Christiansen et al. (1995).

Readers are encouraged to envision the benefits of utilizing inverse modeling to evaluate geohydrologic systems when many parameters and complex boundaries, geometries, and material property distributions are considered. Knowledge of the best-fit parameter values and whether they are reasonable or unreasonable promotes detailed evaluation of the physical system and model construction. The various statistical measures indicate whether the available data are sufficient, and can be used to evaluate potential additional data. Correlations, sensitivities, parameter values and confidence intervals can be used to investigate risk of failure, as suggested by Freeze et al. (1992) and papers referenced therein.

In field applications, it is useful to first use inverse methods without prior information so that the modeler can evaluate how much information the heads, flows, concentrations, and so on contribute to the calibration. This will often necessitate the definition of a simple set of parameters, but the analysis will provide substantial understanding of the interrelation between the model and the data. This understanding is crucial to the effective evolution of more complicated parameter definition.

In practice, initial application of inverse models to field problems often do not converge to optimal parameter values because the data are insufficient to estimate the defined parameters or because the model inadequately represents the physics of the system. Evaluation of calculated sensitivities, correlations, weighted residuals, and changes in parameter values provide abundant information with which to diagnose these problems. Possible solutions include estimating fewer parameters, modifying the parameters defined, modifying other aspects of model construction, and collecting additional data. These problems are not the result of using an inverse model, inverse modeling just makes them obvious.

Automated calibration is of even greater benefit when a transient history match is undertaken. In this case, MODFLOWP can be used to incorporate observations of initial steady state conditions and all subsequent transient observations into the parameter estimation in one execution of the code (for example, see Test Case 1 of Hill, 1992, Appendix A).

A user of inverse models should be adept at groundwater modeling and basic statistics. The effort to sharpen these skills will be offset by the expedient calibration and sensitivity analysis, thorough quantitative assessment of the modeling project, and additional time to evaluate alternative conceptual geohydrologic models.

Summary

Tools are now available to facilitate practical inverse modeling. Inverse modeling can improve the quality of groundwater models and yield results that are not readily available through non-automated calibration efforts, while substantially reducing the time required to obtain parameter estimates. Consequently, the modeler has more opportunity to consider additional aspects of the hydrologic system, such as alternative conceptual models. The entire project may span a time period similar to a non-automated calibration approach, and although there is no guarantee that the model will be more accurate, a more thorough, higher quality, more defensible modeling project should result. Inverse modeling reveals parameter correlations, lack of sensitivity of estimated parameters to available data, and shortcomings of inappropriate conceptual models that can be easily overlooked during non-automated calibration. Quantification of the quality of calibration, data shortcomings and needs, and confidence in parameter estimates and predictions are important to communicating the results of modeling studies to managers, regulators, lawyers, and concerned citizens, as well to the modelers themselves. Such quantifications are a natural result of using groundwater modeling.

Acknowledgments

This work was partially supported by the U.S. Army Waterways Experiment Station and the U.S. Geological Survey.

References

Anderman, E.R., M.C. Hill, and E.P. Poeter, 1996, Two-Dimensional Advective Transport in Ground-Water Flow Parameter Estimation, Ground Water, Vol. 34, No. 6., pp. 1001-1009.

Anderson, M.P., and W.W. Woessner, 1992, Applied groundwater modeling simulation of flow and advective transport: Academic Press, 381p.

Beven, K., and A., Binley, 1992, The future of distributed models, Model calibration and uncertainty prediction: Hydrological Processes, v. 6, p 279-298.

Carrera, J. and S.P. Neuman, 1986, Estimation of aquifer parameters under transient and steady-state conditions: Water Resources Research, v. 22, no. 2, p. 199-242.

Christensen, S. And Cooley, R.L., in review, Simultaneous confidence intervals for a steady-state leaky aquifer groundwater flow model, Kovar, K. et al., eds, Proceedings of ModelCARE '96 Conference, Golden, CO.

Christiansen, H, Hill, M.C., Rosbjerg, D., and K.H. Jensen, (1995), Three-dimensional inverse modeling using heads and concentrations at a Danish landfill: Wagner, B.J. and Illangesekare, T., Proceedings of Models for assessing and monitoring groundwater quality, IAHS-INGG XXI General Assembly, Boulder, CO.

Cooley, R.L., and R.L. Naff, 1990, Regression modeling of groundwater flow, USGS TWRI book 3, chap, B4, 232p.

D'Agnese, F.A., C.C. Faunt, M.C. Hill, A.K. Turner, in review, Calibration of the Death Valley regional groundwater flow model using parameter estimation methods and 3D GIS application, Kovar, K. et al., eds, Proceedings of ModelCARE '96 Conference, Golden, CO.

Doherty, J. 1990, MODINV, Australian Center for Tropical Freshwater Resources, Townsville, Australia, 278p.

Doherty, J. 1994, PEST, Watermark Computing, Corinda, Australia, 122p.

Donaldson and Schnabel, 1987, Computational experience with confidence regions and confidence intervals for nonlinear least squares, Technometrics, v. 29, no. 1, pp. 67-87.

Draper, N.R., and H. Smith, 1981, Applied regression analysis (2nd ed.): John Wiley and Sons, New York, 709p.

Freeze, R.A., James, B., Massman, J., Sperling, T. and L. Smith, 1992, Hydrogeological decision analysis, 4, The concept of data worth and its use in the development of site investigation strategies: Ground Water, v. 30, n. 4, p.574-588.

Giacinto, J.F., 1994, An application of MODFLOWP to a superfund case study, in Proceedings of the 1994 Groundwater Modeling Conference, eds. Warner, J.W., and van der Heijde, P, igwmc, Golden, CO, pp 103-110.

Helsel, D.R. and Hirsch, R.M, 1992, Statistical methods in water resources: Elsevier, New York, 522 p.

Hill, M.C., 1990, Preconditioned conjugate-gradient 2 (PCG2), a computer program for solving groundwater flow equations: USGS WRI Report 90-4048, 43p.

Hill, M.C., 1992, A computer program (MODFLOWP) for estimating parameters of a transient, three-dimensional groundwater flow model using nonlinear regression: USGS OFR 91-484, 358p.

Hill, M.C., 1994, Five computer programs for testing weighted residuals and calculating linear confidence and prediction intervals on results from the groundwater parameter-estimation computer program MODFLOWP, USGS OFR 93-481, 81p.

Hill M.C., Cooley R.L., and D.W. Pollock, in review, A controlled experiment in ground-water flow modeling: 1 Calibration using nonlinear regression to estimate parameter values: submitted to journal.

Hoeksema, R.J. and Kitanidis, P.K., 1984, An application of the geostatistical approach to the inverse problem in two-dimensional groundwater modeling: Water Resources Research, v.20 no. 7, p.1003-1020.

Keidser, Allen and Dan Rosjberg, 1991, A comparison of four inverse approaches to groundwater flow and transport parameter identification, Water Resources Research, v. 27, no. 9, pp 2219-2232.

Knopman, D.S. and C.I. Voss, 1989, Multiobjective sampling design for parameter estimation and model discrimination in groundwater solute transport, Water Resources Research, v. 25, no. 10, pp 2245-2258.

McDonald, M.G., and A.W. Harbaugh, 1988, A Modular, three-dimensional finite-difference groundwater flow model: USGS TWRI, Book 6, Chapter A1, 548p.

Olsthoorn, T.N., 1995, Effective parameter optimization for ground-water model calibration: Ground Water, v. 33, n. 1, p. 42-48.

Poeter E.P. and McKenna S.A., 1995, Reducing uncertainty associated with groundwater flow and transport predictions, Ground Water, vol 33, no. 6, pp. 899-904.

Prudic, D.E., 1989, Documentation of a computer program to simulate stream-aquifer relations using a modular, finite-difference groundwater flow model: USGS OFR 88-729, 144p.

RamaRoa, B.S., LaVenue, M.A., Marsily, Ghislain de, and Marietta, M.G., 1995, Pilot point methodology for automated calibration of an ensemble of conditionally simulated transmissivity fields, 1, Theory and computational experiments: Water Resources Research, v. 31, n. 3, p.475-493.

Seber, G.A.F., and C.J. Wild 1989, Nonlinear Regression, John Wiley & Sons, NY, 768p.

Sun, N.Z., 1994, Inverse Problems in Groundwater Modeling, Kluwer Academic Publishers, Boston, 337p.

Tiedeman, C, and S.M. Gorelick, 1992, Analysis of uncertainty in optimal groundwater contaminant capture design: Water Resources Research, v. 29, n. 7, p. 2139-2153.

Vechia, A.V. and Cooley, R.L., 1987, Simultaneous confidence intervals and prediction intervals for nonlinear regression models with application to a groundwater flow model, Water Resources Research, v. 23, no. 7, pp 1237-1250.

Xiang, Y., Sykes J.F., and N.R. Thomson, 1993, A composite L1 parameter estimator for model fitting in groundwater flow and solute transport simulation. Water Resources Research, v 29. n. 6, pp. 1661-1673.

Yager, R.M., 1993, Simulated three-dimensional groundwater flow in the Lockport Group, a fractured dolomite aquifer near Niagra Falls, New York: USGS WRI Report 92-4189, 43p.

Yeh W.W.G., 1986, Review of parameter identification procedures in groundwater hydrology -- The inverse problem, Water Resources Research, v. 22, no. 2, pp. 95-108.

Yoon, Y.S., and W.W.G. Yeh, 1976, Parameter identification on an inhomogeneous medium with finite element method, Journal of the Society of Petroleum Engineers, v. 16, no. 4, pp217-226.

End Notes

⁽³⁾Ideally, model errors are negligible, and basic regression theory is based on that concept (Draper and Smith, 1981; Seber and Wild, 1989). However, recent work by Hill et al (in review) indicates that for groundwater problems, accumulated model error that is not dominated by a few model errors produces random residuals that are normaly distributed. This suggests model error with such characteristics can be represented by the variances, and therefore the weights.