Implementing an anisotropic and spatially varying Matern model covariance with smoothing filters
- While known to be an important aspect of geostatistical simulations and inverse problems, an a priori model covariance can be difficult to specify and implement, especially where that model covariance is both anisotropic and spatially varying. The popular Matern covariance function is extended to handle such complications, and is implemented as a cascade of numerical solutions to partial differential equations. In effect, each solution is equivalent to application of an anisotropic and spatially varying smoothing filter. Suitable filter coefficients can be obtained from auxiliary data, such as seismic images. An example with simulated porosities demonstrates the effective use of a Matern model covariance implemented in this way.
- Hale, D., 2013, CWP Report 815.
- [Report]
Smooth dynamic warping

- Dynamic time warping is a simple classic method for aligning two sampled functions of time. In applications to seismic traces, the sequence of time shifts computed by this method may increase or decrease rapidly in time (and space). However, when related to integrals of subsurface parameters, these variations in time shifts are often smooth. A new method for smooth dynamic warping exploits this inherent smoothness to increase the accuracy of time shift estimates, especially where differences between seismic traces to be aligned are not limited to time shifts. The new method requires only a few simple modifications to the classic method, and can be easily extended to multidimensional image warping as well. In an application to registration of PP and PS images, we used smooth dynamic warping to compute times shifts that vary smoothly in both time and space, and are significantly more accurate than those computed using the classic method.
- Hale, D., & S. Compton, 2013, CWP Report 764.
- [Report]
Fault surfaces and fault throws from 3D seismic images
- A condensed SEG Expanded Abstract of the following report.
- Hale, D., 2012, 82nd Annual International Meeting, Society of Exploration Geophysicists.
- [Expanded Abstract]
Fault surfaces and fault throws from 3D seismic images
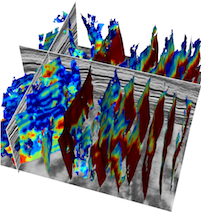
- A new method for processing 3D seismic images yields images of fault likelihoods and corresponding fault strikes and dips. A second process automatically extracts from those images fault surfaces represented by meshes of quadrilaterals. A third process uses differences between seismic image sample values alongside those fault surfaces to automatically estimate fault throw vectors. While some of the faults found in one 3D seismic image have an unusual conical shape, displays of unfaulted images illustrate the fidelity of the estimated fault surfaces and fault throw vectors.
- Hale, D., 2012, CWP Report 721.
- [Report]
Dynamic warping of seismic images
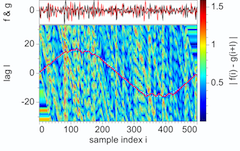
- The problem of estimating relative time (or depth) shifts between two seismic images is ubiquitous in seismic data processing. This problem is especially difficult where shifts are large and vary rapidly with time and space, and where images are contaminated with noise. I propose a solution to this problem that is a simple extension of the classic dynamic time warping algorithm for speech recognition. This new dynamic image warping method for estimating shifts is more accurate than methods based on crosscorrelation of windowed images where shifts vary significantly within the windows.
- Hale, D., 2012, CWP Report 723.
- [Report]
Structure-oriented bilateral filtering

- A condensed SEG Expanded Abstract of the following report.
- Hale, D., 2011, 81st Annual International Meeting, Society of Exploration Geophysicists.
- [Expanded Abstract]
Structure-oriented bilateral filtering

- Bilateral filtering is widely used to enhance photographic images, but in most implementations is poorly suited to seismic images. A bilateral filter consists of two filter kernels. By replacing one of those kernels with a smoothing filter that conforms to image structures, we obtain a bilateral filter suitable for seismic image processing. Examples and comparison with conventional edge-preserving smoothing illustrate both advantages and disadvantages of structure-oriented bilateral filtering.
- Hale, D., 2011, CWP Report 695.
- [Report]
Tensor-guided interpolation on non-planar surfaces
-
In blended-neighbor interpolation of scattered data, a
tensor field represents a model of spatial correlation that
is both anisotropic and spatially varying. In effect, this
tensor field defines a non-Euclidean metric, a measure of
distance that varies with direction and location. The
tensors may be derived from secondary data, such as images.
- Hale, D., 2011, CWP Report 696.
- [Report]
Image-guided 3D interpolation of borehole data

- A condensed SEG Expanded Abstract of the following report.
- Hale, D., 2010, 80th Annual International Meeting, Society of Exploration Geophysicists.
- [Expanded Abstract]
Image-guided 3D interpolation of borehole data
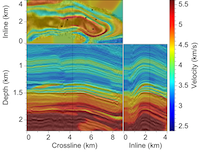
- A blended neighbor method for image-guided interpolation enables resampling of borehole data onto a uniform 3D sampling grid, without picking horizons and without flattening seismic images. Borehole measurements gridded in this way become new 3D images of subsurface properties. Property values conform to geologic layers and faults apparent in the seismic image that guided the interpolation.
- The freely available Teapot Dome data set, which includes a 3D seismic image, horizons picked from that image, and numerous well logs, provides an ideal demonstration of image-guided interpolation of borehole data. In this example, seismic horizons picked by others coincide with thin layers apparent in the new 3D images of interpolated borehole data, even though the horizons were not used in the interpolation process.
- Hale, D., 2010, CWP Report 656.
- [Report]
Image-guided blended neighbor interpolation of scattered data

- A condensed SEG Expanded Abstract of the following report.
- Hale, D., 2009, 79th Annual International Meeting, Society of Exploration Geophysicists.
- [Expanded Abstract]
Image-guided blended neighbor interpolation

- Uniformly sampled images are often used to interpolate other data acquired more sparsely with an entirely different mode of measurement. For example, downhole tools enable geophysical properties to be measured with high precision near boreholes that are scattered spatially, and less precise seismic images acquired at the earth's surface are used to interpolate those properties at locations far away from the boreholes. Image-guided interpolation is designed specifically to enhance this process.
- Most existing methods for interpolation require distances from points where data will be interpolated to nearby points where data are known. Image-guided interpolation requires non-Euclidean distances in metric tensor fields that represent the coherence, orientations and shapes of features in images. This requirement leads to a new method for interpolating scattered data that I call blended neighbor interpolation. For simple Euclidean distances, blended neighbor interpolation resembles the classic natural neighbor interpolation.
- Hale, D., 2009, CWP Report 634.
- [Report]
Structure-oriented smoothing and semblance
- Smoothing along structures apparent in seismic images can enhance these structural features while preserving important discontinuities such as faults or channels. Filters appropriate for such smoothing must seamlessly adapt to variations in the orientation and coherence of image features. I describe an implementation of smoothing filters that does this and is both computationally efficient and simple to implement.
- Structure-oriented filters lead naturally to the computation of structure-oriented semblance, an attribute commonly used to highlight discontinuities in seismic images. Semblance is defined in this paper as simply the ratio of a squared smoothed-image to a smoothed squared-image. This definition of semblance generalizes that commonly used today, because an unlimited variety of smoothing filters can be used to compute the numerator and denominator images in the semblance ratio. The smoothing filters described in this paper yield an especially flexible method for computing structure-oriented semblance.
- Hale, D., 2009, CWP Report 635.
- [Report]
Apparent horizontal displacements in time-lapse seismic images
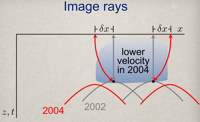
- In addition to vertical time shifts commonly observed in time-lapse seismic images, horizontal displacements are apparent as well. These apparent horizontal displacements may be small relatively to seismic wavelengths, perhaps only 5 m at depths of 5 km, but they consistently suggest an outward lateral expansion of images away from a compacting reservoir.
- It is well known that apparent vertical displacements are caused mostly by a decrease in seismic wave velocities above compacting reservoirs. Those same velocity changes contribute to horizontal displacements. This contribution can be computed from the velocity changes that, in turn, can be estimated from measured vertical displacements. Horizontal displacements computed in this way are similar to those measured, and this similarity suggests that horizontal as well as vertical displacements may be largely due to velocity changes.
- Hale, D., B. Cox & P. Hatchell, 2008, 78th Annual International Meeting, Society of Exploration Geophysicists.
- [Expanded Abstract]
A method for estimating apparent displacement vectors from time-lapse seismic images

- Reliable estimates of vertical, inline and crossline components of apparent displacements in time-lapse seismic images are difficult to obtain for two reasons. First, features in 3-D seismic images tend to be locally planar, and components of displacement within the planes of such features are poorly resolved. Second, searching directly for peaks in 3-D cross-correlations is less robust, more complicated, and computationally more costly than searching for peaks of 1-D cross-correlations. We estimate all three components of displacement with a process designed to mitigate these two problems. We address the first problem by computing for each image sample a local phase-correlation instead of a local cross-correlation. We address the second problem with a cyclic sequence of searches for peaks of correlations computed for lags constrained to one of the three axes of our images.
- Hale, D., 2007, CWP Report 566.
- [Report]
Local dip filtering with directional Laplacians

- Local dip filters attenuate or enhance features with a specified dip that may vary for each image sample. Because these multi-dimensional filters change with each sample, they should have a small number of coefficients that can be computed efficiently from local dips. They should handle features that are vertical as well as horizontal. They should have efficient and stable inverses that facilitate the design and application of more discriminate notch filters. Local dip filters constructed from approximations to directional Laplacians have these properties and are easily implemented in any number of dimensions.
- Hale, D., 2007, CWP Report 567.
- [Report]
An efficient method for computing local cross-correlations of multi-dimensional signals

- Consider two multi-dimensional digital signals, each with S samples. For some number of lags L (L much less than S), the cost of computing a single cross-correlation of these two signals is proportional to S×L. By exploiting several properties of Gaussian windows, we can compute S local cross-correlations, again with computational cost proportional to S×L. Here, local means the cross-correlation of signals after applying a Gaussian window centered on a single sample. Computational cost is independent of the size of the window.
- Hale, D., 2006, CWP Report 544.
- [Report]
Seamless local prediction filtering

- An efficient method for computing local auto-correlations leads to a new method for local adaptive prediction or prediction error filtering of multi-dimensional images. Using a conjugate-gradient method for least-squares optimization, we compute a different prediction filter for each sample in an image. These adaptive prediction filters preserve locally coherent signals, while attenuating random noise.
- Hale, D., 2006, CWP Report 545.
- [Report]
Recursive Gaussian filters
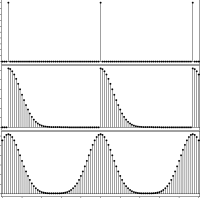
- Gaussian or Gaussian derivative filtering is in several ways optimal for applications requiring low-pass filters or running averages. For short filters with lengths of a dozen samples or so, direct convolution with a finite-length approximation to a Gaussian is the best implementation. However, for longer filters such as those used in computing running averages, recursive implementations may be much more efficient. Based on the filter length, we select one of two popular methods for designing and implementing recursive Gaussian filters.
- Hale, D., 2006, CWP Report 546.
- [Report]
Meshing for velocity modeling and ray tracing in complex velocity fields
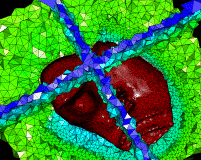
- We automatically generate meshes of subsurface velocity structures from finely-sampled uniform velocity grids without providing external additional constraints such as horizons and faults. Unlike uniform grids, these new meshes provide a topological framework that enables rapid editing of velocity models, while facilitating numerical tasks such as seismic modeling and inversion.
- Rüger, A., & Hale, D., 2004, 74th Annual International Meeting, Society of Exploration Geophysicists.
- [Expanded Abstract]
Seismic interpretation with fluid flow simulation

- We construct simple reservoir models with a small number of flow units, such as geologic layers and fault blocks. We call these units tanks and connect them with tubes. For such simple models, we may interactively adjust reservoir properties, such as porosities of tanks and transmissibilities of tubes, and then simulate fluid flow during seismic interpretation. Numerical experiments suggest that parameters we estimate for coarse tanks & tubes models are meaningful; specifically, they may be used to constrain more detailed models.
- Hale, D., Killough, J., & Emanuel, J., 2004, 74th Annual International Meeting, Society of Exploration Geophysicists.
- [Expanded Abstract]
Seismic interpretation using global image segmentation

- A first step in seismic interpretation is seismic image segmentation. For most seismic images, with incompletely or poorly imaged faults and horizons, global methods for segmentation are more robust than local event tracking or region growing methods often used today. The disadvantage of global image segmentation methods has been their relatively high computational cost. We reduce this cost by applying these methods to a space-filling mesh aligned automatically with features in seismic images. The mesh makes global segmentation of 3-D seismic images feasible.
- Hale, D., & Emanuel, J., 2003, 73th Annual International Meeting, Society of Exploration Geophysicists.
- [Expanded Abstract]
Atomic meshing of seismic images

- Today's work cycle from seismic imaging to reservoir simulation requires a variety of data structures - simple arrays, triangulated surfaces, non-manifold frameworks, corner-point grids, etc. - to represent the earth's subsurface. Conversions among these different representations are both time consuming and error prone. Using simple image processing techniques, we automatically align a lattice of points (atoms) with horizons and faults in a seismic image. Connecting these points yields an unstructured space-filling polyhedral (atomic) mesh. This single data structure can integrate multiple tasks, such as seismic interpretation, reservoir characterization, and flow simulation, thereby reducing work cycle times and errors.
- Hale, D., & Emanuel, J., 2002, 72th Annual International Meeting, Society of Exploration Geophysicists.
- [Expanded Abstract]
Atomic meshes — from seismic imaging to reservoir simulation

- Seismically imaged horizons and faults often correspond to discontinuities in subsurface properties, such as permeability. We automatically align a lattice of points (atoms) either on or alongside such features. 3-D Delaunay triangulation of atoms aligned on image features yields a tetrahedral mesh, with triangular faces of tetrahedra coincident with subsurface discontinuities. Alternatively, the same triangulation of atoms aligned alongside image features yields a dual Voronoi polyhedral mesh in which polygonal faces coincide with subsurface discontinuities. Either mesh is suitable for fluid flow simulation.
- Hale, D., 2002, Proceedings of the 8th European Conference on the Mathematics of Oil Recovery.
- [Paper]
Atomic images — a method for meshing digital images

- By combining a digital image with a lattice of points called atoms, in which atom coordinates are computed to minimize a potential energy function of the combination, we obtain a mesh suitable for further computations. Each atom in the lattice contributes a potential function to an atomic potential field. The image represents another potential field. Total potential energy of the lattice is a weighted sum of the atomic and image potential fields, evaluated at atom coordinates. Beginning with a pseudo-regular lattice, a generic optimization algorithm moves atoms to minimize this total potential energy. After optimization, we connect the atoms to form a mesh that tends to be aligned with image features.
- Hale, D., 2001, Proceedings of the 10th International Meshing Roundtable, p. 85-196.
- [Paper]